
分析 容易根据已知条件得到f(x)-g(x)为增函数,而f(x)+g(x)的单调性不能判断,可根据增函数、减函数的定义证明f(x)-g(x)为增函数:设任意的x1,x2∈D,作差比较f(x1)-g(x1)与f(x2)-g(x2)的大小关系,需利用上f(x),g(x)在D上的单调性,从而证出f(x1)-g(x1)<f(x2)-g(x2),便得出f(x)-g(x)为增函数.
解答 解:f(x)-g(x)为增函数,f(x)+g(x)不一定为增函数,比如f(x)=x,g(x)=-x;
证明f(x)-g(x)为增函数:设x1,x2∈D,且x1<x2,则:
∵f(x)在D上为增函数,g(x)在D上为减函数;
∴f(x1)<f(x2),g(x1)>g(x2);
设F(x)=f(x)-g(x),则:
F(x1)-F(x2)=f(x1)-g(x1)-f(x2)+g(x2)=[f(x1)-f(x2)]+[g(x2)-g(x1)]<0;
∴F(x1)<F(x2);
∴F(x)在D上为增函数;
即f(x)-g(x)在D上为增函数.
点评 考查增函数、减函数的定义,以及根据增函数的定义证明一个函数为增函数的方法和过程,作差比较F(x1)与F(x2)大小的方法,以及增函数和减函数定义的运用.


科目:高中数学 来源: 题型:选择题
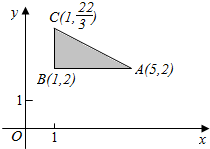 如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(阴影部分且包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,+∞) | D. | (-∞,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | -7 | C. | 11 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{507}{256}$ | B. | $\frac{507}{128}$ | C. | $\frac{509}{128}$ | D. | $\frac{509}{256}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com