
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,AD⊥CD,AB∥CD,AB=3,AD=4,AE=5,![]() .
.
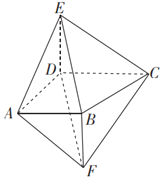
(1)证明:DF∥平面BCE.
(2)求A到平面BEDF的距离,并求四棱锥A﹣BEDF的体积.
【答案】(1)见解析(2)12
【解析】
(1)由DE⊥平面ABCD推出DE⊥AD,勾股定理求出DE,同理由BF⊥平面ABCD求出BF,利用线面垂直的性质推出DE∥BF,结合![]() 推出
推出![]() ,即可证明线面平行;(2)等体积法列出
,即可证明线面平行;(2)等体积法列出![]() ,即可求得A到平面BEDF的距离,四棱锥A﹣BEDF的体积V
,即可求得A到平面BEDF的距离,四棱锥A﹣BEDF的体积V![]() ,代入相应值求解即可.
,代入相应值求解即可.
(1)证明:∵DE⊥平面ABCD,∴DE⊥AD,
∵AD=4,AE=5,∴DE![]() 3,
3,
∵BF⊥平面ABCD,∴BF⊥AB,
∵AB=3,AF![]() ,可得BF
,可得BF![]() 3,
3,
又DE⊥平面ABCD,BF⊥平面ABCD,∴DE∥BF,
又BF=DE,∴四边形BEDF为平行四边形,故DF∥BE,
∵BE平面BCE,DF![]() 平面BCE,
平面BCE,
∴DF∥平面BCE;
(2)设A到平面BEDF的距离为h,
由已知可得,△DAB是以∠DAB为直角的直角三角形,且AB=3,AD=4,
则BD=5,又DE⊥平面ABCD,且DE=3,
由VE﹣ADB=VA﹣BDE,得![]() ,
,
得h![]() ,即A到平面BEDF的距离为
,即A到平面BEDF的距离为![]() ;
;
四棱锥A﹣BEDF的体积V![]() 12.
12.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为椭圆的左焦点、右顶点和下顶点,
分别为椭圆的左焦点、右顶点和下顶点,![]() 的面积为
的面积为![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(1)求椭圆的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且
,且![]() (点
(点![]() 为坐标原点),求
为坐标原点),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() ,
,![]() ,给出以下四个命题:①
,给出以下四个命题:①![]() 为偶函数;②
为偶函数;②![]() 为偶函数;③
为偶函数;③![]() 的最小值为0;④
的最小值为0;④![]() 有两个零点.其中真命题的是( ).
有两个零点.其中真命题的是( ).
A.②④B.①③C.①③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为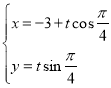 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 是曲线
是曲线![]() 上的任意一点,当点
上的任意一点,当点![]() 到直线
到直线![]() 的距离最大时,求经过点
的距离最大时,求经过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确领导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.甲、乙两个地区采取防护措施后,统计了从2月7日到2月13日一周的新增“新冠肺炎”确诊人数,绘制成如下折线图:
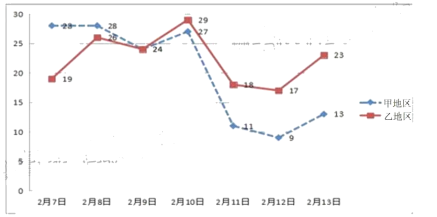
(1)根据图中甲、乙两个地区折线图的信息,写出你认为最重要的两个统计结论;
(2)治疗“新冠肺炎”药品的研发成了当务之急,某药企计划对甲地区的![]() 项目或乙地区的
项目或乙地区的![]() 项目投入研发资金,经过评估,对于
项目投入研发资金,经过评估,对于![]() 项目,每投资十万元,一年后利润是l.38万元、1.18万元、l.14万元的概率分别为
项目,每投资十万元,一年后利润是l.38万元、1.18万元、l.14万元的概率分别为![]() 、
、![]() 、
、![]() ;对于
;对于![]() 项目,利润与产品价格的调整有关,已知
项目,利润与产品价格的调整有关,已知![]() 项目产品价格在一年内进行2次独立的调整,每次价格调整中,产品价格下调的概率都是
项目产品价格在一年内进行2次独立的调整,每次价格调整中,产品价格下调的概率都是![]() ,记
,记![]() 项目一年内产品价格的下调次数为
项目一年内产品价格的下调次数为![]() ,每投资十万元,
,每投资十万元,![]() 取0、1、2时,一年后相应利润是1.4万元、1.25万元、0.6万元.记对
取0、1、2时,一年后相应利润是1.4万元、1.25万元、0.6万元.记对![]() 项目投资十万元,一年后利润的随机变量为
项目投资十万元,一年后利润的随机变量为![]() ,记对
,记对![]() 项目投资十万元,一年后利润的随机变量为
项目投资十万元,一年后利润的随机变量为![]() .
.
(i)求![]() ,
,![]() 的概率分布列和数学期望
的概率分布列和数学期望![]() ,
,![]() ;
;
(ii)如果你是投资决策者,将做出怎样的决策?请写出决策理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点F且倾斜角为
的焦点F且倾斜角为![]() 的直线交抛物线于AB两点,交其准线于点C,且|AF|=|FC|,|BC|=2.
的直线交抛物线于AB两点,交其准线于点C,且|AF|=|FC|,|BC|=2.
(1)求抛物线C的方程;
(2)直线l交抛物线C于DE两点,且这两点位于x轴两侧,与x轴交于点M,若![]() ·
·![]() 求
求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com