
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ).
).
(1)利用“五点法”,完成以下表格,并画出函数f(x)在一个周期上的图象;
(2)求函数f(x)的单调递减区间和对称中心的坐标;
(3)如何由y=cosx的图象变换得到f(x)的图象.
2x- | 0 |
| π |
| 2π |
x | |||||
f(x) |
【答案】(1)详见解析(2)f(x)的单调减区间为:(![]() +kπ,
+kπ,![]() +kπ),k∈Z,对称中心为(
+kπ),k∈Z,对称中心为(![]() +
+![]() ,0),k∈Z;(3)详见解析
,0),k∈Z;(3)详见解析
【解析】
(1)利用“五点法”作出函数f(x)在一个周期上的图象(先列表,再画图);(2)利用余弦函数的单调性和对称性即可得解.(3)由条件利用y=Acos(ωx+φ)的图象变换规律,得出结论.
(1)列表如下:
2x- | 0 |
| π |
| 2π |
x |
|
|
|
|
|
f(x) |
| 0 | - | 0 |
|
画图如下:
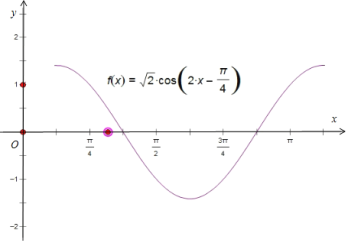
(2)令2kπ<2x-![]() <π+2kπ,k∈Z,得:
<π+2kπ,k∈Z,得:![]() +kπ<x<
+kπ<x<![]() +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的单调减区间为:(![]() +kπ,
+kπ,![]() +kπ),k∈Z,
+kπ),k∈Z,
令2x-![]() =
=![]() +kπ,k∈Z,得:x=
+kπ,k∈Z,得:x=![]() +
+![]() ,k∈Z,
,k∈Z,
∴f(x)的对称中心为(![]() +
+![]() ,0),k∈Z,
,0),k∈Z,
(3)图象先向右平移![]() 个单位长度再纵坐标不变,横坐标缩小为原来的
个单位长度再纵坐标不变,横坐标缩小为原来的![]() 倍,最后横坐标不变,纵坐标伸长为原来的
倍,最后横坐标不变,纵坐标伸长为原来的![]() 倍
倍


科目:高中数学 来源: 题型:
【题目】据研究,甲磁盘受到病毒感染,感染的量y(单位: 比特数)与时间x(单位:秒)的函数关系是![]() ,乙磁盘受到病毒感染,感染的量y(单位: 比特数)与时间x(单位:秒)的函数关系是
,乙磁盘受到病毒感染,感染的量y(单位: 比特数)与时间x(单位:秒)的函数关系是![]() ,显然当
,显然当![]() 时,甲磁盘受到病毒感染增长率比乙磁盘受到病毒感染增长率大.试根据上述事实提炼一个不等式,并证明之.
时,甲磁盘受到病毒感染增长率比乙磁盘受到病毒感染增长率大.试根据上述事实提炼一个不等式,并证明之.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知k∈R,直线l1:x+ky=0过定点P,直线l2:kx﹣y﹣2k+2=0过定点Q,两直线交于点M,则|MP|+|MQ|的最大值是( )
A.2 ![]()
B.4
C.4 ![]()
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.
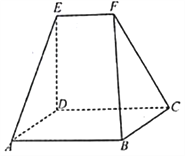
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x∈(-1,1)),有下列结论:
(x∈(-1,1)),有下列结论:
(1)x∈(-1,1),等式f(-x)+f(x)=0恒成立;
(2)m∈[0,+∞),方程|f(x)|=m有两个不等实数根;
(3)x1,x2∈(-1,1),若x1≠x2,则一定有f(x1)≠f(x2);
(4)存在无数多个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有三个零点
则其中正确结论的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①线性回归方程对应的直线![]() 至少经过其样本数据点
至少经过其样本数据点![]() 中的一个点;
中的一个点;
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于![]() ;
;
③在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]()
![]() ,若
,若![]() 位于区域
位于区域![]() 内的概率为
内的概率为![]() ,则
,则![]() 位于区域
位于区域![]() 内的概率为
内的概率为![]() ;
;
④对分类变量![]() 与
与![]() 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“![]() 与
与![]() 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
A. ①④ B. ②④ C. ①③ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}的前n项和为Sn , 且S2=6,S4=30,n∈N* , 数列{bn}满足bnbn+1=an , b1=1
(1)求an , bn;
(2)求数列{bn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣3≤0,x∈R},B={x|m﹣1≤x≤m+1,x∈R,m∈R}
(1)若A∩B=[1,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com