
【题目】已知椭圆![]() ,右顶点为
,右顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() ,椭圆
,椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() (
(![]() 在
在![]() 之间),求
之间),求![]() 与
与![]() 面积之比的取值范围.
面积之比的取值范围.
科目:高中数学 来源: 题型:
【题目】自新型冠状病毒疫情爆发以来,人们时刻关注疫情,特别是治愈率,治愈率![]() 累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第
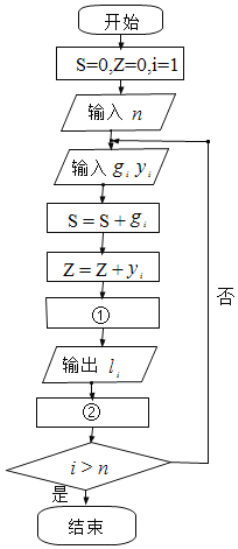
累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第![]() 天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
![]() :第
:第![]() 天新增确诊人数;
天新增确诊人数;![]() :第
:第![]() 天新增治愈人数;
天新增治愈人数;![]() :第
:第![]() 天治愈率
天治愈率
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
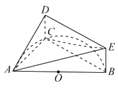
(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

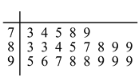
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与过点
与过点![]() 的直线
的直线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,探究:以
,探究:以![]() 为直径的圆是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
为直径的圆是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
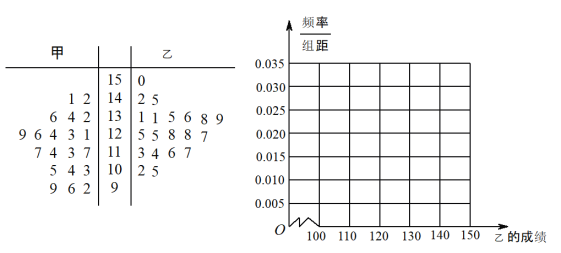
(1)根据茎叶图求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩的频率分布直方图补充完整;
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设选出的2个成绩中含甲的成绩的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
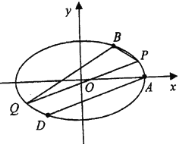
【题目】已知椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆上,点
在椭圆上,点![]() 与点
与点![]() 关于原点对称.
关于原点对称.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求经过点![]() ,
,![]() 且和
且和![]() 轴相切的圆的方程;
轴相切的圆的方程;
(3)若![]() ,
,![]() 是椭圆上异于
是椭圆上异于![]() ,
,![]() 的两个点,且
的两个点,且![]() ,点
,点![]() 在直线
在直线![]() 的上方,试判断
的上方,试判断![]() 的平分线是否经过
的平分线是否经过![]() 轴上的一个定点?若是,求出该定点坐标;若不是,请说明理由.
轴上的一个定点?若是,求出该定点坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com