
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,在以![]() 为顶点的五面体中,底面
为顶点的五面体中,底面![]() 是矩形,
是矩形, ![]() .
.
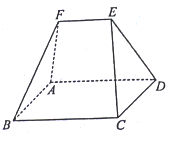
(1)证明: ![]() 平面
平面![]() ;
;
(2)在中国古代数学经典著作《九章算术》中,称图中所示的五面体![]() 为“刍甍”(chúméng),书中将刍甍
为“刍甍”(chúméng),书中将刍甍![]() 的体积求法表述为:
的体积求法表述为:
术曰:倍下袤,上袤从之,以广乘之,又以高乘之,六而一.其意思是:若刍甍![]() 的“下袤”
的“下袤” ![]() 的长为
的长为![]() ,“上袤”
,“上袤” ![]() 的长为
的长为![]() ,“广”
,“广” ![]() 的长为
的长为![]() ,“高”即“点
,“高”即“点![]() 到平面
到平面![]() 的距离”为
的距离”为![]() ,则刍甍
,则刍甍![]() 的体积
的体积![]() 的计算公式为:
的计算公式为: ![]() ,证明该体积公式.
,证明该体积公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线![]() ,直线
,直线![]() 过定点(—2,2),且斜率为
过定点(—2,2),且斜率为![]() .以O为极点,x轴的正半轴为极轴建立极坐标系.
.以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的直角坐标方程以及直线l的参数方程;
的直角坐标方程以及直线l的参数方程;
(2)点P在曲线![]() 上,当
上,当![]() 时,求点P到直线l的最小距离并求点P的坐标
时,求点P到直线l的最小距离并求点P的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着小汽车的普及,“驾驶证”已经成为现代人“必考”证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,需要通过四个科目的考试,其中科目二为场地考试在每一次报名中,每个学员有![]() 次参加科目二考试的机会(这
次参加科目二考试的机会(这![]() 次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试,或
次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试,或![]() 次都没有通过,则需要重新报名),其中前
次都没有通过,则需要重新报名),其中前![]() 次参加科目二考试免费,若前
次参加科目二考试免费,若前![]() 次都没有通过,则以后每次参加科目二考试都需要交
次都没有通过,则以后每次参加科目二考试都需要交![]() 元的补考费.某驾校通过几年的资料统计,得到如下结论:男性学员参加科目二考试,每次通过的概率均为
元的补考费.某驾校通过几年的资料统计,得到如下结论:男性学员参加科目二考试,每次通过的概率均为![]() ,女性学员参加科目二考试,每次通过的概率均为
,女性学员参加科目二考试,每次通过的概率均为![]() .现有一对夫妻同时报名参加驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
.现有一对夫妻同时报名参加驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)求这对夫妻在本次报名中参加科目二考试产生的补考费用之和为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
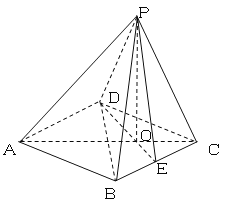
【题目】如图,已知四棱锥P-ABCD的底面是边长为2的菱形,∠BCD=60°,点E是BC边
的中点,AC,DE交于点O,![]() ,且PO⊥平面ABCD.
,且PO⊥平面ABCD.
(1)求证:PD⊥BC;
(2)在线段AP上找一点F,使得BF∥平面PDE,并求此时四面体PDEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com