
【题目】为了解某市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩![]() ;(精确到个位)
;(精确到个位)
(2)研究发现,本次检测的理科数学成绩![]() 近似服从正态分布
近似服从正态分布![]() (
(![]() ,
,![]() 约为
约为![]() ),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占
),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占![]() .
.
(ⅰ)估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分?(精确到个位)
(ⅱ)从该市高三理科学生中随机抽取![]() 人,记理科数学成绩能达到自主招生分数要求的人数为
人,记理科数学成绩能达到自主招生分数要求的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .(说明:
.(说明:![]() 表示
表示![]() 的概率.参考数据:
的概率.参考数据:![]() )
)
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1.记
的首项为1.记![]() .
.
(1)若![]() 为常数列,求
为常数列,求![]() 的值:
的值:
(2)若![]() 为公比为2的等比数列,求
为公比为2的等比数列,求![]() 的解析式:
的解析式:
(3)是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立?若存在,求出数列
都成立?若存在,求出数列![]() 的通项公式:若不存在,请说明理由.
的通项公式:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的标准方程为:![]() ,该椭圆经过点P(1,
,该椭圆经过点P(1,![]() ),且离心率为
),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆![]() 长轴上一点S(1,0)作两条互相垂直的弦AB、CD.若弦AB、CD的中点分别为M、N,证明:直线MN恒过定点.
长轴上一点S(1,0)作两条互相垂直的弦AB、CD.若弦AB、CD的中点分别为M、N,证明:直线MN恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级有学生480名,对他们进行政治面貌和性别的调查,其结果如下:
性别 | 团员 | 群众 |
男 |
| 80 |
女 | 180 |
|
(1)若随机抽取一人,是团员的概率为![]() ,求
,求![]() ,
,![]() ;
;
(2)在团员学生中,按性别用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名团员中任选2人,求两人中至多有1个女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺公司要对某种工艺品深加工,已知每个工艺品进价为20元,每个的加工费为n元,销售单价为x元.根据市场调查,须有![]() ,
,![]() ,
,![]() ,同时日销售量m(单位:个)与
,同时日销售量m(单位:个)与![]() 成正比.当每个工艺品的销售单价为29元时,日销售量为1000个.
成正比.当每个工艺品的销售单价为29元时,日销售量为1000个.
(1)写出日销售利润y(单位:元)与x的函数关系式;
(2)当每个工艺品的加工费用为5元时,要使该公司的日销售利润为100万元,试确定销售单价x的值.(提示:函数![]() 与
与![]() 的图象在
的图象在![]() 上有且只有一个公共点)
上有且只有一个公共点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与
与
椭圆![]() 的一个交点为
的一个交点为![]() ,点
,点![]()
是![]() 的焦点,且
的焦点,且![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
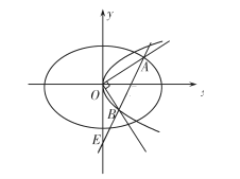
(2)设![]() 为坐标原点,在第一象限内,椭圆
为坐标原点,在第一象限内,椭圆![]() 上是否存在点
上是否存在点![]() ,使过
,使过![]() 作
作![]() 的垂线交抛物线
的垂线交抛物线![]() 于
于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ?若存在,求出点
?若存在,求出点![]() 的坐标和
的坐标和![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com