
【题目】已知点![]() 是椭圆
是椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为左焦点,点
为左焦点,点![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,直线
的任意一点,直线![]() 与过点
与过点![]() 且垂直于
且垂直于![]() 轴的直线
轴的直线![]() 交于点
交于点![]() ,直线
,直线![]() 于点
于点![]() .
.
(1)求证:直线![]() 与直线
与直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)若直线![]() 过焦点
过焦点![]() ,
, ![]() ,求实数
,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为![]() ,
, ![]() 是椭圆上一点,若
是椭圆上一点,若![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过右焦点
过右焦点![]() (不与
(不与![]() 轴重合)且与椭圆相交于不同的两点
轴重合)且与椭圆相交于不同的两点![]() ,在
,在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() 的值为定值?若存在,写出
的值为定值?若存在,写出![]() 点的坐标(不必求出定值);若不存在,说明理由.
点的坐标(不必求出定值);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)为定义R在的偶函数,当0≤x≤2时,y= ![]() ;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
;当x>2时,y=f(x)的图象是顶点在p(3,4),且过点A(2,3)的抛物线的一部分.
(1)求函数f(x)的解析式;
(2)在下面的直角坐标系中直接画出函数f(x)的图象,写出函数f(x)的单调区间(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
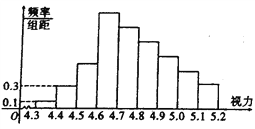
【题目】统计全国高三学生的视力情况,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频率成等比数列,后6组的频率成等差数列.
(Ⅰ)求出视力在[4.7,4.8]的频率;
(Ⅱ)现从全国的高三学生中随机地抽取4人,用![]() 表示视力在[4.3,4.7]的学生人数,写出
表示视力在[4.3,4.7]的学生人数,写出![]() 的分布列,并求出
的分布列,并求出![]() 的期望与方差.
的期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为对数函数,并且它的图象经过点(2 ![]() ,
, ![]() ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[ ![]() ,16]上的最小值.
,16]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣3x2+a(6﹣a)x+c.
(1)当c=19时,解关于a的不等式f(1)>0;
(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(4x+1)﹣x,g(x)=log2a+log2(2x﹣ ![]() )(a>0,x>1).
)(a>0,x>1).
(1)证明函数f(x)为偶函数;
(2)若函数f(x)﹣g(x)只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在![]() 的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
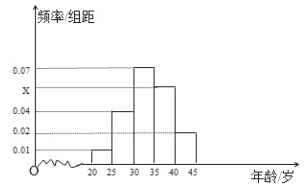
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com