
【题目】若函数![]() 在
在![]() 时,函数值y的取值区间恰为[
时,函数值y的取值区间恰为[![]() ],就称区间
],就称区间![]() 为
为![]() 的一个“倒域区间”.定义在
的一个“倒域区间”.定义在![]() 上的奇函数
上的奇函数![]() ,当
,当![]() 时,
时,![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 在
在![]() 内的“倒域区间”;
内的“倒域区间”;
(Ⅲ)若函数![]() 在定义域内所有“倒域区间”上的图像作为函数
在定义域内所有“倒域区间”上的图像作为函数![]() =
=![]() 的图像,是否存在实数
的图像,是否存在实数![]() ,使集合
,使集合![]() 恰含有2个元素.
恰含有2个元素.
【答案】(Ⅰ) (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)![]()
【解析】
试题(1)运用奇偶性得出 ;(2)得出方程组问题
;(2)得出方程组问题
(3)![]() ,利用方程思想求解
,利用方程思想求解 ,m应当使方程
,m应当使方程![]() ,在
,在 内恰有一个实数根,并且使方程
内恰有一个实数根,并且使方程![]() ,在
,在 内恰有一个实数
内恰有一个实数
试题解析:(Ⅰ)当![]() 时,
时,![]()

(Ⅱ)设1≤![]() <
<![]() ≤2,∵
≤2,∵![]() 在
在![]() 上递减,
上递减,
∴ 整理得
整理得
 ,解得
,解得 .
.
∴![]() 在
在![]() 内的“倒域区间”为
内的“倒域区间”为 .
.
(Ⅲ)∵![]() 在
在![]() 时,函数值y的取值区间恰为
时,函数值y的取值区间恰为![]() ,其中
,其中![]()
∴![]() ,∴
,∴![]() 同号.只考虑0<
同号.只考虑0<![]() <
<![]() ≤2或-2≤
≤2或-2≤![]() <
<![]() <0
<0
当0<![]() <
<![]() ≤2时,根据
≤2时,根据![]() 的图像知,
的图像知,![]() 最大值为1,
最大值为1,![]() ,
,
∴1≤![]() <
<![]() ≤2,由(Ⅱ)知
≤2,由(Ⅱ)知![]() 在
在![]() 内的“倒域区间”为
内的“倒域区间”为 ;
;
当-2≤![]() <
<![]() <0时间,
<0时间,![]() 最小值为-1,
最小值为-1,![]() ,
,
∴![]() ,同理知
,同理知![]() 在
在![]() 内的“倒域区间”为
内的“倒域区间”为 .
.

依题意:抛物线与函数![]() 的图象有两个交点时,一个交点在第一象限,一个交点在第三象限.因此,
的图象有两个交点时,一个交点在第一象限,一个交点在第三象限.因此,![]() 应当使方程
应当使方程![]() ,在
,在 内恰有一个实数根,并且使方程
内恰有一个实数根,并且使方程![]() ,在
,在 内恰有一个实数
内恰有一个实数
由方程![]() 在
在 内恰有一根知
内恰有一根知![]() ;
;
由方程![]() 在
在 内恰有一根知
内恰有一根知![]() ,
,
综上:![]() =-2.
=-2.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某高校自主招生一次面试成绩的茎叶图和频率分布直方图均收到了不同程度的损坏,其可见部分信息如下,据此解答下列问题:
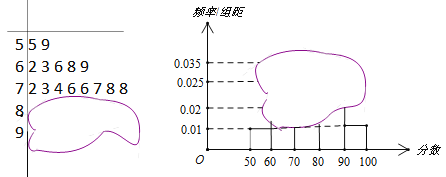
(1)求参加此次高校自主招生面试的总人数![]() 、面试成绩的中位数及分数在
、面试成绩的中位数及分数在![]() 内的人数;
内的人数;
(2)若从面试成绩在![]() 内的学生中任选三人进行随机复查,求恰好有二人分数在
内的学生中任选三人进行随机复查,求恰好有二人分数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商场销售某种商品的经验表明,该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求![]() 的值;
的值;
(2) 若商品的成品为3元/千克, 试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大
的值,使商场每日销售该商品所获得的利润最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的![]() ,都有
,都有![]() ;②对于任意的
;②对于任意的![]() 都有
都有![]() ③函数
③函数![]() 的图象关于y轴对称,则下列结论中正确的是( )
的图象关于y轴对称,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对100名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在55名男性驾驶员中,平均车速超过![]() 的有40人,不超过
的有40人,不超过![]() 的有15人;在45名女性驾驶员中,平均车速超过
的有15人;在45名女性驾驶员中,平均车速超过![]() 的有20人,不超过
的有20人,不超过![]() 的有25人.
的有25人.
(1)完成下面的列联表,并判断是否有![]() %的把握认为平均车速超过
%的把握认为平均车速超过![]() 的人与性别有关.
的人与性别有关.
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为男性且车速超过![]() 的车辆数为X,若每次抽取的结果是相互独立的,求X的分布列和数学期望.
的车辆数为X,若每次抽取的结果是相互独立的,求X的分布列和数学期望.
参考公式与数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用极坐标与直角坐标的互化公式可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
,消去参数![]() 可知曲线
可知曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,由直线
的圆,由直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得: ![]() ;则曲线C的方程为
;则曲线C的方程为![]() , 再次利用极坐标与直角坐标的互化公式可得
, 再次利用极坐标与直角坐标的互化公式可得
可得曲线C的极坐标方程.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面积的最大值.
面积的最大值.
试题解析:(1)由题意可知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,直线
的圆,直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得:  ;可知曲线C的方程为
;可知曲线C的方程为![]() ,
,
所以曲线C的极坐标方程为![]() ,
,
即![]() .
.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
当![]() 时,
时, ![]() ,
,
所以△MON面积的最大值为![]() .
.
【题型】解答题
【结束】
23
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 上顶点为A,右焦点为F,直线
上顶点为A,右焦点为F,直线![]() 与圆
与圆![]() 相切,其中
相切,其中![]() .
.
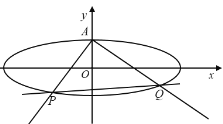
(1)求椭圆的方程;
(2)不过点A的动直线l与椭圆C相交于P,Q两点,且![]() ,证明:动直线l过定点,并且求出该定点坐标.
,证明:动直线l过定点,并且求出该定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com