
分析 设$\overrightarrow{OA}$=$\overrightarrow{α}$,$\overrightarrow{OB}$=$\overrightarrow{β}$,则$\overrightarrow{AB}$=$\overrightarrow{β}$-$\overrightarrow{α}$,△OAB为等腰三角形,且∠AOB=120°,∠OAB=∠OBA=30°,求得$\overrightarrow{α}•\overrightarrow{β}$=$\sqrt{3}$•$\sqrt{3}$•cos120°=-$\frac{3}{2}$,再根据 $|{t\overrightarrow α+\frac{1-t}{2}\overrightarrow β}|$=$\sqrt{{(t•\overrightarrow{a}+\frac{1-t}{2}•\overrightarrow{β})}^{2}}$,利用二次函数的性质求得它的范围.
解答 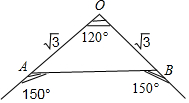 解:∵平面向量$|{\overrightarrow α}|=|{\overrightarrow β}|=\sqrt{3}$且$\overrightarrow α$与 $\overrightarrow β-\overrightarrow α$的夹角为150°,
解:∵平面向量$|{\overrightarrow α}|=|{\overrightarrow β}|=\sqrt{3}$且$\overrightarrow α$与 $\overrightarrow β-\overrightarrow α$的夹角为150°,
如图,设$\overrightarrow{OA}$=$\overrightarrow{α}$,$\overrightarrow{OB}$=$\overrightarrow{β}$,则$\overrightarrow{AB}$=$\overrightarrow{β}$-$\overrightarrow{α}$,
∴△OAB为等腰三角形,且∠AOB=120°,∠OAB=∠OBA=30°,
∴$\overrightarrow{α}•\overrightarrow{β}$=$\sqrt{3}$•$\sqrt{3}$•cos120°=-$\frac{3}{2}$,
∴$|{t\overrightarrow α+\frac{1-t}{2}\overrightarrow β}|$=$\sqrt{{(t•\overrightarrow{a}+\frac{1-t}{2}•\overrightarrow{β})}^{2}}$=$\sqrt{{3t}^{2}+t(1-t)•\overrightarrow{α}•\overrightarrow{β}{+(\frac{1-t}{2})}^{2}•3}$
=$\sqrt{{3t}^{2}+t(1-t)•(-\frac{3}{2})+\frac{3}{4}•{(t}^{2}-2t+1)}$=$\sqrt{\frac{21}{4}{(t}^{2}-\frac{4}{7}t)+\frac{3}{4}}$=$\sqrt{\frac{21}{4}{•(t-\frac{2}{7})}^{2}+\frac{9}{28}}$≥$\frac{3\sqrt{7}}{14}$,
故答案为:[$\frac{3\sqrt{7}}{14}$,+∞).
点评 本题考查了向量的夹角、直角三角形的边角关系、向量共线定理,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
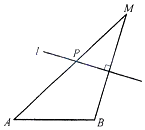 如图,已知A、B是两个顶点,且$AB=2\sqrt{3}$,动点M到点A的距离是4,线段MB的垂直平分线l交MA于点P.
如图,已知A、B是两个顶点,且$AB=2\sqrt{3}$,动点M到点A的距离是4,线段MB的垂直平分线l交MA于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | a3>b3 | C. | a2>b2 | D. | $\frac{b}{a}+\frac{a}{b}>2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | $3\sqrt{7}$ | C. | $3\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知正方体ABCD-A1B1C1D1的棱长为1,给出下列四个命题:
已知正方体ABCD-A1B1C1D1的棱长为1,给出下列四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
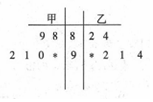 在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”
在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com