练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．下面有四个命题：
    ①函数y=sin2x的最小周期是π；
    ②把函数$y=3sin（{\frac{π}{3}-x}）$的单调区间是$[{-2kπ-\frac{π}{6}，-2kπ+\frac{5π}{6}}]$，k∈Z；
    ③函数$y=tan（{x+\frac{π}{3}}）$的定义域是$\left\{{x\left|{x∈R且x≠2kπ+\frac{π}{6}，k∈Z}\right.}\right\}$；
    ④函数y=tanx的图象的对称中心坐标是（kπ，0），k∈Z．
    其中，正确的是①．（填上所有正确命题的序号）

    分析 对4个选项分别进行判断，即可得出结论．

    解答 解：①函数y=sin2x的最小周期是$\frac{2π}{2}$=π，正确；
    ②由-$\frac{π}{2}$+2kπ≤x-$\frac{π}{3}$≤$\frac{π}{2}$π+2kπ，可得-$\frac{π}{6}$+2kπ≤x≤$\frac{5π}{6}$π+2kπ，可得把函数$y=3sin（{\frac{π}{3}-x}）$的单调减区间是[-$\frac{π}{6}$+2kπ，$\frac{5π}{6}$π+2kπ]，k∈Z，不正确；
    ③由x+$\frac{π}{3}$≠$\frac{π}{2}$+kπ，可得函数$y=tan（{x+\frac{π}{3}}）$的定义域是$\left\{{x\left|{x∈R且x≠2kπ+\frac{π}{6}，k∈Z}\right.}\right\}$，不正确；
    ④函数y=tanx的图象的对称中心坐标是（$\frac{1}{2}$kπ，0），k∈Z，不正确．
    故答案为：①．

    点评 本题考查命题的真假判断，考查学生分析解决问题的能力，知识综合性强．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．下列叙述错误的是（　　）
    A．若事件A发生的概率为P（A），则0≤P（A）≤1
    B．系统抽样是不放回抽样，每个个体被抽到的可能性相等
    C．线性回归直线$\hat y=\hat bx+\hat a$必过点$（\overline x，\overline y）$
    D．对于任意两个事件A和B，都有P（A∪B）=P（A）+P（B）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若A={2，3，4}，B={x|x＜4}，则集合A∩B中的元素个数是（　　）
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在$-\frac{π}{4}≤x≤\frac{π}{4}$，则函数y=tanx的值域为[-1，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．正三棱柱ABC-A1B1C1各棱长均为1，M为CC1的中点，则点B1到截面A1BM的距离为（　　）
    A．$\sqrt{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．（1）计算log25625+lg0.01+ln$\sqrt{e}$-2；
    （2）已知tan（π+α）=3，求$\frac{2cos（π-a）-3sin（π+a）}{4cos（-a）+sin（2π-a）}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

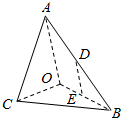    1．如图，在三棱锥AB0C中．AO⊥平面BOC，∠OAB=∠OAC=$\frac{π}{6}$．AB=AC=2．BC=$\sqrt{2}$，D，E分别为AB，OB的中点．
    （1）求O到平面ABC的距离；
    （2）在线段CB上是否存在一点F，使得平面DEF∥平面AOC，若存在，试确定F的位置，并证明此点满足要求；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数$f（x）=a-\frac{4}{{{2^x}+1}}（{a∈R}）$是定义在（-∞，+∞）上的奇函数．
    （1）求a的值，并写出函数f（x）的解析式；
    （2）求证：函数f（x）在上是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知各项均为正数的数列{an}的首项a1=1，sn是数列{an}的前n项和，且满足：
    anSn+1-an+1Sn+an-an+1=λanan+1（λ≠0，n∈N• ）
    （1）若a1，a2，a3成等比数列，求实数λ的值；
    （2）若λ=$\frac{1}{2}$，求Sn．

    查看答案和解析>>

    同步练习册答案