【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且 
bcosA=asinB．
（1）求角A的大小；
（2）若a=6，△ABC的面积是9 ，求三角形边b，c的长．
【答案】
（1）解：在△ABC中， 
bcosA=asinB．
由正弦定理得 
，
∴ 
，又0＜A＜π，
∴ 
（2）解：由S△ABC=9 ，得 
bcsin 
=9 ，即为bc=36，
由余弦定理可得a2=b2+c2﹣2bccosA=（b+c）2﹣2bc﹣2bccos ，
即36=（b+c）2﹣3bc=（b+c）2﹣108，
解得b+c=12，
由 
得 
，
∴三角形边b，c的长都为6
【解析】（1）运用正弦定理和同角的商数关系，由特殊角的三角函数值可得A；（2）运用三角形的面积公式和余弦定理，解方程即可得到所求b，c的值．
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义，需要了解正弦定理:
；余弦定理:
;
;
才能得出正确答案．
口算题天天练系列答案科目：高中数学 来源： 题型：
【题目】如图，已知抛物线y2=4x，过点P（2，0）作斜率分别为k1 ， k2的两条直线，与抛物线相交于点A、B和C、D，且M、N分别是AB、CD的中点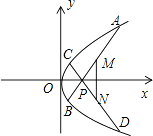 
（1）若k1+k2=0， 
，求线段MN的长；
（2）若k1k2=﹣1，求△PMN面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四组函数，表示同一函数的是（ ）
A.f（x）= 
，g（x）=x
B.f（x）=x，g（x）= 
C.f（x）=lnx2 ， g（x）=2lnx
D.f（x）=logaax（a＞0，a≠1），g（x）= 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示.
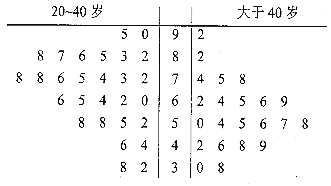
（1）根据茎叶图中的数据完成
列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
（2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，记抽到的2人中年龄大于40岁的市民人数为
，求
的分布列和数学期望.
附：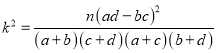 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球.规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得
分，现从盒内任取3个球.
(Ⅰ)求取出的3个球中至少有一个红球的概率；
(Ⅱ)求取出的3个球得分之和恰为1分的概率；
(Ⅲ)设
为取出的3个球中白色球的个数，求
的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
