
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知纵坐标不同的两点![]() ,
,![]() 为椭圆
为椭圆![]() 上的两个点,且
上的两个点,且![]() ,
,![]() ,
,![]() 三点共线,线段
三点共线,线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
科目:高中数学 来源: 题型:
【题目】为庆祝中华人民共和国成立70周年,2019年10月1日晚,金水桥南,百里长街成为舞台,3290名联欢群众演员跟着音乐的旋律,用手中不时变幻色彩的光影屏,流动着拼组出五星红旗、祖国万岁、长城等各式图案和文字.光影潋滟间,以《红旗颂》《我们走在大路上》《在希望的田野上》《领航新时代》四个章节,展现出中华民族从站起来、富起来到强起来的伟大飞跃.在每名演员的手中都有一块光影屏,每块屏有1024颗灯珠,若每个灯珠的开、关各表示一个信息,则每块屏可以表示出不同图案的个数为( )
A.2048B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解疫情期间哈一中高三学生的心理需求,更好的开展高考前的心理健康教育工作,心理老师设计了两个问题,第一个问题是“你出生的月份是奇数吗?”;第二个问题是“你是否需要心理疏导?”.让被调查者在保密的情况下掷一个均匀的骰子,其他人不知道掷骰子的结果,要求:当出现1点或2点时,回答第一个问题;否则回答第二个问题,由于其他人不知道他回答的是哪一个问题,因此,当他回答“是”时,你也无法知道他是否有心理问题,这种调查既保护了他的隐私,也能反映真实情况,可以从调查结果中得到需要的估计,若调查的900名学生中有156人回答“是”,由此可估计我校高三需要心理疏导的学生所占的比例约为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
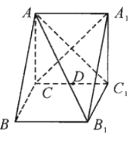
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() //平面
//平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置:若不存在,请说明理由.
的位置:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com