
【题目】已知函数![]()
(1)当a=-2时,求函数f(x)的极值;
(2)若ln[e(x+1)]≥2- f(-x)对任意的x∈[0,+∞)成立,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,E是
,E是![]() 的中点.现将
的中点.现将![]() 沿
沿![]() 翻折,使点A移动至平面
翻折,使点A移动至平面![]() 外的点P.
外的点P.
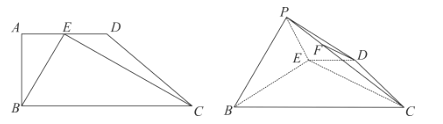
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(x+)(A>0,>0,0<<)的部分图象如图所示,又函数g(x)=f(x+![]() ).
).
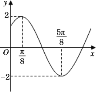
(1)求函数g(x)的单调增区间;
(2)设![]() ABC的内角ABC的对边分别为abc,又c=
ABC的内角ABC的对边分别为abc,又c=![]() ,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
,且锐角C满足g(C)= -1,若sinB=2sinA,,求ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治疗某种疾病,某科研机构研制了甲、乙两种新药,为此进行白鼠试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药一轮的治疗结果得出后,再安排下一轮试验.4轮试验后,就停止试验.甲、乙两种药的治愈率分别是![]() 和
和![]() .
.
(1)若![]() ,求2轮试验后乙药治愈的白鼠比甲药治愈的白鼠多1只的概率;
,求2轮试验后乙药治愈的白鼠比甲药治愈的白鼠多1只的概率;
(2)已知A公司打算投资甲、乙这两种新药的试验耗材费用,甲药和乙药一次试验耗材花费分别为3千元和![]() 千元,每轮试验若甲、乙两种药都治愈或都没有治愈,则该科研机构和A公司各承担该轮试验耗材总费用的50%;若甲药治愈,乙药未治愈,则A公司承担该轮试验耗材总费用的75%,其余由科研机构承担,若甲药未治愈,乙药治愈,则A公司承担该轮试验耗材总费用的25%,其余由科研机构承担.以A公司每轮支付试验耗材费用的期望为标准,求A公司4轮试验结束后支付试验耗材最少费用为多少元?
千元,每轮试验若甲、乙两种药都治愈或都没有治愈,则该科研机构和A公司各承担该轮试验耗材总费用的50%;若甲药治愈,乙药未治愈,则A公司承担该轮试验耗材总费用的75%,其余由科研机构承担,若甲药未治愈,乙药治愈,则A公司承担该轮试验耗材总费用的25%,其余由科研机构承担.以A公司每轮支付试验耗材费用的期望为标准,求A公司4轮试验结束后支付试验耗材最少费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com