
【题目】已知数列{an}满足: ![]() ,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1). (Ⅰ)求数列{an},{bn}的通项公式
,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1). (Ⅰ)求数列{an},{bn}的通项公式
(Ⅱ)证明:数列{bn}中的任意三项不可能成等差数列.
【答案】解:(Ⅰ)由题意可知, ![]()
令cn=1﹣an2,则 ![]()
又 ![]() ,则数列{cn}是首项为
,则数列{cn}是首项为 ![]() ,公比为
,公比为 ![]() 的等比数列,即
的等比数列,即 ![]() ,
,
故 ![]() ,
,
又 ![]() ,anan+1<0
,anan+1<0
故 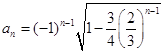
因为 ![]() =
= ![]() ,
,
故 ![]()
(Ⅱ)假设数列{bn}存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,
由于数列{bn}是首项为 ![]() ,公比为
,公比为 ![]() 的等比数列,
的等比数列,
于是有2bs=br+bt成立,则只有可能有2br=bs+bt成立,
∴ ![]()
化简整理后可得,2=( ![]() )r﹣s+(
)r﹣s+( ![]() )t﹣s,
)t﹣s,
由于r<s<t,且为整数,故上式不可能成立,导致矛盾.
故数列{bn}中任意三项不可能成等差数列.
【解析】(1)对 ![]() 化简整理得
化简整理得 ![]() ,令cn=1﹣an2,进而可推断数列{cn}是首项为
,令cn=1﹣an2,进而可推断数列{cn}是首项为 ![]() ,公比为
,公比为 ![]() 的等比数列,根据等比数列通项公式求得cn,则a2n可得,进而根据anan+1<0求得an.(2)假设数列{bn}存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,由于数列{bn}为等比数列,于是有br>bs>bt,则只有可能有2bs=br+bt成立,代入通项公式,化简整理后发现等式左边为2,右边为分数,故上式不可能成立,导致矛盾.
的等比数列,根据等比数列通项公式求得cn,则a2n可得,进而根据anan+1<0求得an.(2)假设数列{bn}存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,由于数列{bn}为等比数列,于是有br>bs>bt,则只有可能有2bs=br+bt成立,代入通项公式,化简整理后发现等式左边为2,右边为分数,故上式不可能成立,导致矛盾.
【考点精析】掌握数列的定义和表示和等差数列的性质是解答本题的根本,需要知道数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,给出以下四个结论:
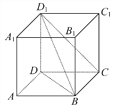
①D1C∥平面A1ABB1;②A1D1与平面BCD1相交;
③AD⊥平面D1DB;④平面BCD1⊥平面A1ABB1.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
灯管数/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx,g(x)=ax+ ![]() ,函数f(x)的图象与x轴的交点也在函数g(x)的图象上,且在此点有公切线. (Ⅰ)求a、b的值;
,函数f(x)的图象与x轴的交点也在函数g(x)的图象上,且在此点有公切线. (Ⅰ)求a、b的值;
(Ⅱ)试比较f(x)与g(x)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x2 . (Ⅰ) 求f(x)的单调区间;
(Ⅱ) 若f(x)的定义域为[﹣1,m]时,值域为[﹣4,0],求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前55个圈中的●的个数是( )
A.10
B.9
C.8
D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com