
图17
A.![]() B.9 C.
B.9 C.![]() D.4
D.4
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源:教材完全解读 高中数学 必修5(人教B版课标版) 人教B版课标版 题型:044
一次机器人足球比赛中,甲队1号机器人由A点开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动,如图所示,已知AB=![]() ,AD=17 dm,∠BAC=45°,若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?
,AD=17 dm,∠BAC=45°,若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?

查看答案和解析>>
科目:高中数学 来源: 题型:
图2-5-17
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)![]() 还成立吗?如果成立,请给出证明;如果不成立,请说明理由.(2)请找出S△ABD、S△BED和S△BDC间的关系式,并给出证明.
还成立吗?如果成立,请给出证明;如果不成立,请说明理由.(2)请找出S△ABD、S△BED和S△BDC间的关系式,并给出证明.
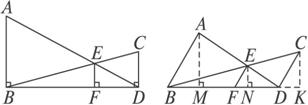
(1) (2)
图1-2-17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com