
【题目】如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD,
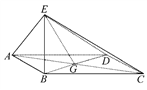
(1)证明:平面AEC⊥平面BED.
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为![]() ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
【答案】(1)见解析(2)3+2![]() .
.
【解析】试题分析:(1)由菱形性质得AC⊥BD.再由线面垂直性质得AC⊥BE,因此AC⊥平面BED.最后根据面面垂直判定定理得结论(2)先确定各面形状,再根据勾股定理求对应量,最后根据面积公式求各面面积,和为侧面积
试题解析:(1)因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,所以AC⊥BE,又BD∩BE=B,故AC⊥平面BED.
又AC平面AEC,所以平面AEC⊥平面BED.
(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=![]() x,GB=GD=
x,GB=GD=![]() .
.
因为AE⊥EC,所以在Rt△AEC中,可得EG=![]() x.
x.
由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=![]() x.
x.
由已知得,三棱锥E-ACD的体积
VE-ACD=![]() ×
×![]() AC·GD·BE=
AC·GD·BE=![]() x3=
x3=![]() .
.
故x=2.从而可得AE=EC=ED=![]() .
.
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为![]() .
.
故三棱锥E-ACD的侧面积为3+2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称为“局部奇函数”
,则称为“局部奇函数”
(1)已知二次函数![]() (
(![]() 且
且![]() ),试判断
),试判断![]() 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域为
为定义域为![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
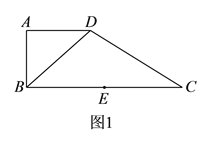
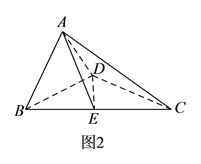
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是长方形,侧棱
是长方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过D作
,过D作![]() 于F,过F作
于F,过F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)证明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
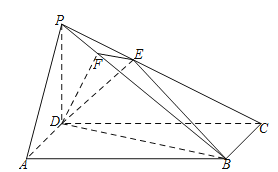
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名;乙协会的运动员
名;乙协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名.从这
名.从这![]() 名运动员中随机选择
名运动员中随机选择![]() 人参加比赛.
人参加比赛.
(1)设![]() 为事件“选出的
为事件“选出的![]() 人中恰有
人中恰有![]() 名种子选手,且这
名种子选手,且这![]() 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的
为选出的![]() 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1-x),(a>0,a≠1).
(1)设a=2,函数f(x)的定义域为[3,63],求f(x)的最值;
(2)求使f(x)-g(x)>0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com