
【题目】在如图所示直角梯形ABCD中,AB∥DC,∠A=90°,AB=AD=2DC=4,画出该梯形的直观图A′B′C′D′,并写出其做法(要求保留作图过程的痕迹.)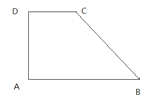
【答案】解:(1)在已知的直角梯形ABCD中,以AB所在直线为x轴,垂直于AB的腰AD所在直线为y轴建立平面直角坐标系;
(2)画相应的x′轴和y′轴,使得∠x′O′y′=45°,在x′轴上取O′B′=AB,在y′轴上取O′D′=AD,过D′作x′轴的平行线l,在l上沿x′轴正方向取点C′使得D′C′=DC;
(3)连接B′C′,所得四边形O′B′C′D′就是直角梯形ABCD的直观图.
【解析】根据平面图形的直观图的画法,即可得出结论.
【考点精析】本题主要考查了斜二测法画直观图的相关知识点,需要掌握斜二测画法的步骤:(1)平行于坐标轴的线依然平行于坐标轴;(2)平行于y轴的线长度变半,平行于x,z轴的线长度不变;(3)画法要写好才能正确解答此题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 A﹣BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4. 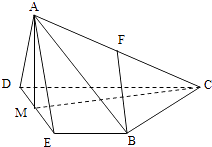
(1)求证:平面 ADE⊥平面BCD;
(2)求证:FB∥平面ADE;
(3)求四棱锥A﹣BCDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0.当直线l被圆C截得的弦长为 ![]() 时,求
时,求
(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C过点P(1,1),且与⊙M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过点P(﹣2,1),
(1)若直线l与直线x+y﹣1=0平行,求直线l的方程;
(2)若点A(﹣1,﹣2)到直线l的距离为1,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2(x﹣ ![]() )﹣
)﹣ ![]() sin2x+1
sin2x+1
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)当x∈( ![]() ,
, ![]() )时,若f(x)≥log2t恒成立,求 t的取值范围.
)时,若f(x)≥log2t恒成立,求 t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 的焦距为2.
的焦距为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,过
,过![]() 作
作![]() 轴且与椭圆
轴且与椭圆![]() 交于另一点
交于另一点![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,求证:三点
的右焦点,求证:三点![]() 在同一条直线上.
在同一条直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com