
(3分)(2011•重庆)在圆x2+y2﹣2x﹣6y=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A. | B. | C. | D. |
B
解析试题分析:把圆的方程化为标准方程后,找出圆心坐标与圆的半径,根据图形可知,过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦BD,根据两点间的距离公式求出ME的长度,根据垂径定理得到E为BD的中点,在直角三角形BME中,根据勾股定理求出BE,则BD=2BE,然后利用AC与BD的乘积的一半即可求出四边形ABCD的面积.
解:把圆的方程化为标准方程得:(x﹣1)2+(y﹣3)2=10,
则圆心坐标为(1,3),半径为 ,
,
根据题意画出图象,如图所示:
由图象可知:过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦,则AC=2 ,MB=
,MB= ,ME=
,ME= =
=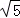 ,
,
所以BD=2BE=2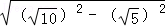 =2
=2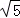 ,又AC⊥BD,
,又AC⊥BD,
所以四边形ABCD的面积S= AC•BD=
AC•BD= ×2
×2 ×2
×2 =10
=10 .
.
故选B
点评:此题考查学生掌握垂径定理及勾股定理的应用,灵活运用两点间的距离公式化简求值,是一道中档题.学生做题时注意对角线垂直的四边形的面积等于对角线乘积的一半.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:单选题
过点M(1,2)的直线l将圆(x-2)2+y2=9分成两段弧,当其中的劣弧最短时,直线的方程是( )
| A.x=1 | B.y=1 |
| C.x-y+1=0 | D.x-2y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
(2013•重庆)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 ﹣4 ﹣4 | B.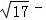 1 1 | C.6﹣2 | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com