
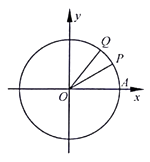
【题目】设A是单位圆O和x轴正半轴的交点,P,Q是圆O上两点,O为坐标原点,∠AOP= ![]() ,∠AOQ=α,α∈[0,
,∠AOQ=α,α∈[0, ![]() ].
]. 
(1)若Q( ![]() ,
, ![]() ),求cos(α﹣
),求cos(α﹣ ![]() )的值;
)的值;
(2)设函数f(α)=sinα( ![]()
![]() ),求f(α)的值域.
),求f(α)的值域.
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,下列说法正确的是____ (填序号).
(1)直线AC1在平面CC1B1B内.
(2)设正方形ABCD与A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1.
(3)由A、C1、B1确定的平面是ADC1B1.
(4)由A、C1、B1确定的平面与由A、C1、D确定的平面是同一个平面.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=log2x+ax+b(a>0),若存在实数b,使得对任意的x∈[t,t+2](t>0)都有|f(x)|≤1+a,则t的最小值是( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F为双曲线 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )
=1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( ) 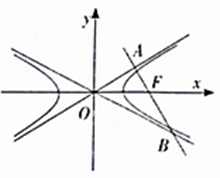
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的一次篮球定点投篮训练中,规定每人最多投3次,在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率为0.25,在B处的命中率为0.8,该同学选择先在A处投一球,以后都在B处投,用X表示该同学投篮训练结束后所得的总分.
(1)求该同学投篮3次的概率;
(2)求随机变量X的数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com