
【题目】已知奇函数y=f(x)定义域是R,当x≥0时,f(x)=x(1﹣x).
(1)求出函数y=f(x)的解析式;
(2)写出函数y=f(x)的单调递增区间.(不用证明,只需直接写出递增区间即可)
【答案】
(1)解:当x<0时,﹣x>0,
∴f(﹣x)=﹣x(1+x).
又因为y=f(x)是奇函数
所以f(x)=﹣f(﹣x)x(1+x).
综上f(x)= ![]()
(2)函数y=f(x)的单调递增区间是[ ![]() ,
, ![]() ]
]
【解析】(1)当x<0时,﹣x>0,则f(﹣x)=﹣x(1+x),再根据y=f(x)是奇函数,则有f(x)=﹣f(﹣x)x(1+x),以分段函数的形式写出解析式,(2)依据(1)中的解析式可写出f(x)的单调区间.
【考点精析】通过灵活运用函数的单调性和函数奇偶性的性质,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥平面PAB,AD∥BC,BC=CD= ![]() AD,E,F分别为线段AD,PD的中点.
AD,E,F分别为线段AD,PD的中点. 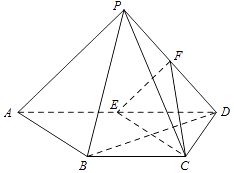
(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)求证:PD⊥平面CEF;
(Ⅲ)写出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2 ![]() ,且AC,BD交于点O,E是PB上任意一点.
,且AC,BD交于点O,E是PB上任意一点.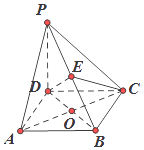
(1)求证:AC⊥DE
(2)已知二面角A﹣PB﹣D的余弦值为 ![]() ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a4=6,a6=10.
(1)求数列{an}的通项公式;
(2)设等比数列{bn}各项均为正数,其前n项和Tn , 若b3=a3 , T2=3,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(1﹣t),且x ![]() 时,f(x)=﹣x2 , 则f(3)+f(﹣
时,f(x)=﹣x2 , 则f(3)+f(﹣ ![]() 的值等于( )
的值等于( )
A.﹣ ![]()
B.﹣ ![]()
C.﹣ ![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足f(x+3)=2f(x),当x∈[﹣1,2)时,f(x)= 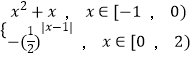 .
.
若存在x∈[﹣4,﹣1),使得不等式t2﹣3t≥4f(x)成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学巨著,内容极为丰富,其中卷六《均输》里有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”(“钱”是古代的一种重量单位),则其中第二人分得的钱数是( )
A.![]()
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 f(x)=2x﹣ ![]() 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(Ⅰ)当a=﹣1时,求函数y=f(x)的值域;
(Ⅱ)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(Ⅲ)求函数y=f(x)在x∈(0,1]上的最大值及最小值,并求出函数取最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+ ![]() (1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.
(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.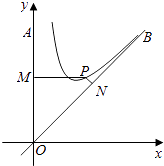
(1)求f(x)解析式;
(2)当x为多少时,总造价f(x)最低?并求出最低造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com