
【题目】在![]() 中,D,E,F分别是边
中,D,E,F分别是边![]() ,
,![]() ,
,![]() 中点,下列说法正确的是( )
中点,下列说法正确的是( )
A.![]()
B.![]()
C.若 ,则
,则![]() 是
是![]() 在
在![]() 的投影向量
的投影向量
D.若点P是线段![]() 上的动点,且满足
上的动点,且满足![]() ,则
,则![]() 的最大值为
的最大值为![]()
【答案】BCD
【解析】
对选项A,B,利用平面向量的加减法即可判断A错误,B正确.对选项C,首先根据已知得到![]() 为
为![]() 的平分线,即
的平分线,即![]() ,再利用平面向量的投影概念即可判断C正确.对选项D,首先根据
,再利用平面向量的投影概念即可判断C正确.对选项D,首先根据![]() 三点共线,设
三点共线,设![]() ,
,![]() ,再根据已知得到
,再根据已知得到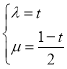 ,从而得到
,从而得到![]() ,即可判断选项D正确.
,即可判断选项D正确.
如图所示:
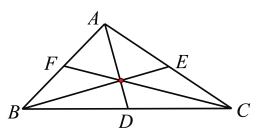
对选项A,![]() ,故A错误.
,故A错误.
对选项B,![]()
![]()
![]() ,故B正确.
,故B正确.
对选项C,![]() ,
,![]() ,
,![]() 分别表示平行于
分别表示平行于![]() ,
,![]() ,
,![]() 的单位向量,
的单位向量,
由平面向量加法可知:![]() 为
为![]() 的平分线表示的向量.
的平分线表示的向量.
因为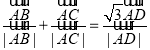 ,所以
,所以![]() 为
为![]() 的平分线,
的平分线,
又因为![]() 为
为![]() 的中线,所以
的中线,所以![]() ,如图所示:
,如图所示:
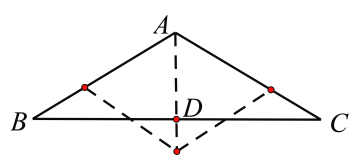
![]() 在
在![]() 的投影为
的投影为 ,
,
所以![]() 是
是![]() 在
在![]() 的投影向量,故选项C正确.
的投影向量,故选项C正确.
对选项D,如图所示:
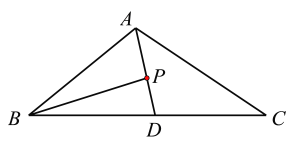
因为![]() 在
在![]() 上,即
上,即![]() 三点共线,
三点共线,
设![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() .
.
因为![]() ,则
,则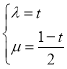 ,
,![]() .
.
令![]() ,
,
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .故选项D正确.
.故选项D正确.
故选:BCD


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②B. ①③④C. ②④D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不共线的向量![]() ,
,![]() 夹角为
夹角为![]() ,且
,且![]() ,
,![]() ,为正实数.
,为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值及对应的x的值,并指出此时向量
的最小值及对应的x的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数m,关于x的方程
为锐角,对于正实数m,关于x的方程![]() 两个不同的正实数解,且
两个不同的正实数解,且![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A.已知直线![]() 和平面
和平面![]() ,若点
,若点![]() ,点
,点![]() 且
且![]() ,
,![]() ,则
,则![]()
B.若三条直线两两相交,则三条直线确定一个平面
C.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则
,则![]() 内的所有直线与
内的所有直线与![]() 都不相交
都不相交
D.若直线![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,则l至少与
,则l至少与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,BCD是边长为![]() 的等边三角形,
的等边三角形,![]() ,二面角A﹣BC﹣D的大小为θ,且
,二面角A﹣BC﹣D的大小为θ,且![]() ,则三棱锥A﹣BCD体积的最大值为( )
,则三棱锥A﹣BCD体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率是40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定l,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下10组随机数:907 966 191 925 271 431 932 458 569 683.
据此估计,该运动员三次投篮恰有两次命中的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,我市积极打造“绿城”的创建目标,使城市环境绿韵萦绕,使市民生活绿意盎然.有效增加城区绿化面积,提高城区绿化覆盖率,提升城市形象品位.林业部门推广种植甲、乙两种树苗,并对甲、乙两种树苗各抽测了10株树苗的高度(单位:厘米),数据如下面的茎叶图:

(1)根据茎叶图求甲、乙两种树苗的平均高度;
(2)根据茎叶图,计算甲、乙两种树苗的高度的方差,运用统计学知识分析比较甲、乙两种树苗高度整齐情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 的底面为菱形,
的底面为菱形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,求
,求![]() 的长.
的长.
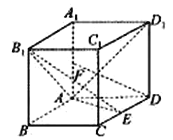
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)设![]() 为
为![]() 的中点,根据平几知识可得四边形
的中点,根据平几知识可得四边形![]() 是平行四边形,即得
是平行四边形,即得![]() ,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面
,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面![]() 一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得
一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得![]() 的长.
的长.
试题解析:(1)证明:设![]() 为
为![]() 的中点,连
的中点,连![]()
因为![]()
![]()
![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]()
![]()
![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
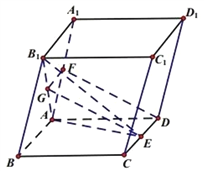
(2)因为![]() 是菱形,且
是菱形,且![]() ,
,
所以![]() 是等边三角形
是等边三角形
取![]() 中点
中点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
, ![]()
建立如图的空间直角坐标系,令![]() ,
,
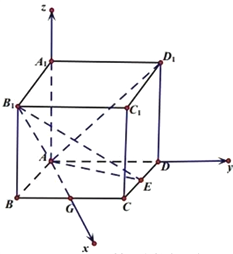
则![]() ,
, 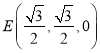 ,
, ![]() ,
, ![]() ,
,
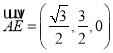 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() 且
且![]() ,
,
取![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则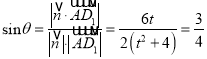 ,
,
解得![]() ,故线段
,故线段![]() 的长为2.
的长为2.
【题型】解答题
【结束】
20
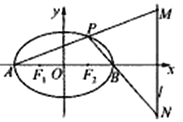
【题目】椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,若椭圆过点
,若椭圆过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆的左、右顶点,
为椭圆的左、右顶点, ![]() (
(![]() )为椭圆上一动点,设直线
)为椭圆上一动点,设直线![]() 分别交直线
分别交直线![]() :
: ![]() 于点
于点![]() ,判断线段
,判断线段![]() 为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com