分析:(1)因为P是棱BB1的中点,可想到取AB1的中点M,由三角形中位线知识证明四边形PCEM是平行四边形,由此可得
PC∥EM,然后利用线面平行的判定即可得到结论;
(2)题目给出了三棱锥A1-AB1E的体积是6,借助于等积法可求AB的长度;
(3)以A为坐标原点,建立空间直角坐标系,利用平面法向量所成角的余弦值求二面角的余弦值.
解答:(1)证明:取AB
1的中点M,连结PM,ME.
则PM∥BA∥CE,
PM=AB=CE.
即四边形PCEM是平行四边形,所以PC∥EM.
又EM?平面AEB
1,PC?平面AEB
1.
∴CP∥平面AEB
1;
(2)解:由题意
VA1-AB1E=VE-AB1A1.
点E到平面AB
1A
1的距离是AD=3,
S△AB1A1=•AB•AA1=AB•2=AB.
所以
•3•AB=6,即AB=6;
(3)解:以A为坐标原点,分别以AB,AD,AA
1所在直线为x轴,y轴,z轴建立空间直角坐标系A-xyz.
则A(0,0,0),B
1(6,0,2),E(3,3,0),
=(6,0,2),=(3,3,0).
设平面AB
1E的法向量为
=(x,y,z).
由
,得
,取x=1,得y=-1,z=-3.
所以
=(1,-1,-3).
由平面ABB
1的一个法向量为
=(0,1,0).
并设二面角B-AB
1-E的大小为α,
则cosα=
|cos<,>|=
||=
.
所以二面角B-AB
1-E的余弦值为
.
点评:本题考查了线面平行的判定,关键是寻求定理成立的条件,常借助于三角形的中位线处理.训练了等积法求点到面的距离或线段的长度,考查了利用平面法向量求二面角的余弦值,是中档题.

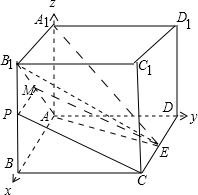
 (2013•湛江二模)如图,在长方体ABCD一A1B1C1D1中,AA1=2,AD=3,E为CD中点,三棱 锥A1-AB1E的体积是6.
(2013•湛江二模)如图,在长方体ABCD一A1B1C1D1中,AA1=2,AD=3,E为CD中点,三棱 锥A1-AB1E的体积是6.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 (2013•湛江二模)如图,已知平面上直线l1∥l2,A、B分别是l1、l2上的动点,C是l1,l2之间一定点,C到l1的距离CM=1,C到l2的距离CN=
(2013•湛江二模)如图,已知平面上直线l1∥l2,A、B分别是l1、l2上的动点,C是l1,l2之间一定点,C到l1的距离CM=1,C到l2的距离CN=