在等差数列{an}中,a5=0.3,a12=3.1,求a18+a19+a20+a21+a22的值.
【答案】
分析:解法1,由条件建立方程组可得数列的首项为a
1,公差为d,由数列项与公差的关系代入可得答案;
解法2,由题意可得公差,进而可得a
20,而a
18+a
19+a
20+a
21+a
22等于5a
1+95d,代入可得答案.
解答:解:设数列的首项为a
1,公差为d
则
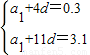
,解得

∴a
18+a
19+a
20+a
21+a
22=5a
1+17d+18d+19d+20d+21d=5a
1+95d=31.5
法2:设数列的公差为d,则
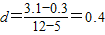
,
∴a
20=a
12+8d=3.1+8×0.4=6.3,
a由等差数列的性质可得:
18+a
19+a
20+a
21+a
22=5a
20=5×6.3=31.5
点评:本题考查等差数列的性质和基本运算,属基础题

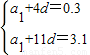 ,解得
,解得
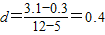 ,
,
