
【题目】已知集合M={x|x2﹣4x+3<0},N={x||x﹣3|≤1}.
(1)求出集合M,N;
(2)试定义一种新集合运算△,使M△N={x|1<x<2};
(3)若有P={x|| ![]() |≥
|≥ ![]() },按(2)的运算,求出(N△M)△P.
},按(2)的运算,求出(N△M)△P.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥V﹣ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.
(Ⅰ)求证:VC∥平面BED;
(Ⅱ)求证:平面VAC⊥平面BED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请200名同学,每人随机写下一个都小于1的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计
的值:先请200名同学,每人随机写下一个都小于1的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计![]() 的值.假如统计结果是m=56,那么可以估计
的值.假如统计结果是m=56,那么可以估计![]() __________.(用分数表示)
__________.(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点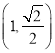 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,ab≠0,给出下面四个命题:①a2+b2≥﹣2ab;② ![]() ≥2;③若a<b,则ac2<bc2;④若
≥2;③若a<b,则ac2<bc2;④若 ![]() .则a>b;其中真命题有( )
.则a>b;其中真命题有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e﹣x , 其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com