分析:(1)建立如图所示的空间直角坐标系D-xyz.求出平面EB
1D的法向量
1,和平面B
1CD的法向量
2,根据两个法向量的数量积为0,互相垂直,得到平面EB
1D⊥平面B
1CD;
(2)由(1)中平面B
1CD的法向量
2,结合平面CDE的法向量
=(0,0,1),代入向量夹角公式,即可求出二面角B
1-CD-E的大小;
(3)由(1)中平面B
1CD的法向量
2,代入点E到平面B
1CD的距离公式d=
,可得点E到平面B
1CD的距离.
解答: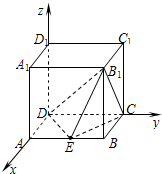
证明:(1)建立如图所示的空间直角坐标系D-xyz.
∵E(2,1,0),C(0,2,0),B
1(2,2,2)
∴
=(0, 1, 2),
=(-2, -1, 0).
设平面EB
1D的法向量为
1=(x,y,z),则
即
,不妨取
1=(1,-2,1).
同理,平面B
1CD的法向量
2=(-1,0,1).…(3分)
∵
1•
2=-1+1=0,∴平面EB
1D⊥平面B
1CD. …(4分)
(2)解由(1)得平面B
1CD的法向量
2=(-1,0,1),
又平面CDE的法向量
=(0,0,1),∴
cos<,>===…(7分)
∴二面角E-B
1C-D的大小为45°. …(8分)
(3)由(1)得平面B
1CD的法向量
2=(-1,0,1),又
=(2,1,0)∴点E到平面B
1CD的距离为
==…(12分)
说明:采用其它方法进行解答的,按每小题(3分),根据作答情况酌情给分.
点评:本题考查的知识点是用空间向量表示平面间的夹角,点到平面之间的距离计算,向量语言表述面面垂直,平行关系,其中建立适当的空间直角坐标系,将空间点,线,面之间的关系问题转化为向量问题是解答此类问题的关键.

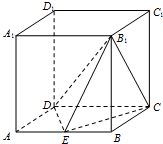 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为AB的中点. 证明:(1)建立如图所示的空间直角坐标系D-xyz.
证明:(1)建立如图所示的空间直角坐标系D-xyz.

 考前必练系列答案
考前必练系列答案



