练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，函数（）.

    （1）讨论的单调性；

    （2）证明：当时，.

    （3）证明：当时，.

    【答案】（1）答案不唯一，具体见解析（2）证明见解析（3）证明见解析

    【解析】

    （1）求出的定义域，导函数，对参数、分类讨论得到答案.

    （2）设函数，求导说明函数的单调性，求出函数的最大值，即可得证.

    （3）由（1）可知，可得，即又即可得证.

    （1）解：的定义域为，，

    当，时，，则在上单调递增；

    当，时，令，得，令，得，则在上单调递减，在上单调递增；

    当，时，，则在上单调递减；

    当，时，令，得，令，得，则在上单调递增，在上单调递减；

    （2）证明：设函数，则.

    因为，所以，，

    则，从而在上单调递减，

    所以，即.

    （3）证明：当时，.

    由（1）知，，所以，

    即.

    当时，，，

    则，

    即，

    又，

    所以，

    即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在党中央的正确指导下，通过全国人民的齐心协力，特别是全体一线医护人员的奋力救治，二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报，甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下：

    根据图中甲、乙两省的数字特征进行比对，通过比较把你得到最重要的两个结论写在答案纸指定的空白处.

    ①_________________________________________________.

    ②_________________________________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为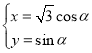（为参数），以原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程与曲线的直角坐标方程；

    （2）设为曲线上位于第一，二象限的两个动点，且，射线交曲线分别于，求面积的最小值，并求此时四边形的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在直角梯形中，，，，，，两点分别在线段，上运动，且.将三角形沿折起，使点到达的位置，且平面平面.

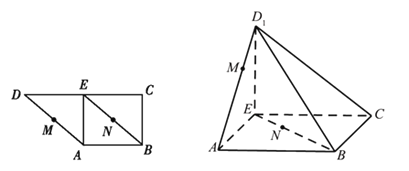
    （1）判断直线与平面的位置关系并证明；

    （2）证明：的长度最短时，，分别为和的中点；

    （3）当的长度最短时，求平面与平面所成角（锐角）的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥中，，，，，点分别为的中点．

    （1）证明：平面∥平面；

    （2）若，求异面直线与所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）当时，设函数在区间上的最小值为，求；

    （2）设，若函数有两个极值点，且，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD是矩形，平面ABCD⊥平面BCE，BE⊥EC.

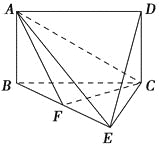
    (1)求证：平面AEC⊥平面ABE；

    (2)点F在BE上．若DE∥平面ACF，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示：

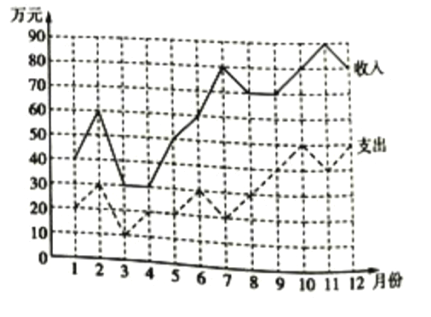
    根据该折线图可知，下列说法错误的是（ ）

    A. 该超市2018年的12个月中的7月份的收益最高

    B. 该超市2018年的12个月中的4月份的收益最低

    C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益

    D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元

    查看答案和解析>>

    同步练习册答案