
在立体图形P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,Q是PC中点.
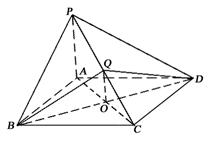 AC,BD交于O点.
AC,BD交于O点.
(Ⅰ)求二面角Q-BD-C的大小:
(Ⅱ)求二面角B-QD-C的大小.
(Ⅰ)解:连QO,则QO∥PA且QO=![]() PA=
PA=![]() AB
AB
∵ PA⊥面ABCD
∴ QO⊥面ABCD
面QBD过QO,
∴ 面QBD⊥面ABCD
故二面角Q-BD-C等于90°.
 (Ⅱ)解:过O作OH⊥QD,垂足为H,连CH.
(Ⅱ)解:过O作OH⊥QD,垂足为H,连CH.
∵ 面QBD⊥面BCD,
又∵ CO⊥BD
CO⊥面QBD
CH在面QBD内的射影是OH
∵ OH⊥QD
∴ CH⊥QD
于是∠OHC是二面角的平面角.
设正方形ABCD边长2,
则OQ=1,OD=![]() ,QD=
,QD=![]() .
.
∵ OH·QD=OQ·OD
∴ OH=![]() .
.
又OC=![]()
在Rt△COH中:tan∠OHC=![]() =
=![]() ·
·![]() =
=![]()
∴ ∠OHC=60°
故二面角B-QD-C等于60°.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型:044
在立体图形
P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,Q是PC中点.AC,BD交于O点.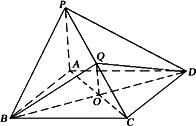
(Ⅰ)求二面角Q-BD-C的大小:
(Ⅱ)求二面角B-QD-C的大小.
查看答案和解析>>
科目:高中数学 来源:重庆市09-10高二下学期质量检测数学试题 题型:解答题
(本小题满分12分)在立体图形P-ABCD中,底面ABCD是正方形,直线PA垂直于底面,且PA=AD,E、F分别是AB、PC的中点.
 (1)求证:
(1)求证: 平面PAD;
平面PAD;
(2)求证:直线 平面PCD.
平面PCD.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省高二上学期第一次月考文科数学卷 题型:解答题
(本题满分12分)
在立体图形P-ABCD中,底面ABCD是一个直角梯形,∠BAD=90°,AD∥BC,
AB=BC=a,AD=PA=2a,E是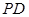 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。
(1)求证:BE⊥PD
(2)求证: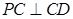
(3)求异面直线AE与CD所成的角.
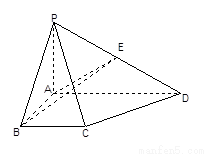
查看答案和解析>>
科目:高中数学 来源:重庆市杨家坪中学09-10高二下学期质量检测数学试题 题型:解答题
(本小题满分12分)在立体图形P-ABCD中,底面ABCD是正方形,直线PA垂直于底面,且PA=AD,E、F分别是AB、PC的中点.  (1)求证:
(1)求证: 平面PAD;
平面PAD;
(2)求证:直线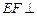 平面PCD.
平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com