
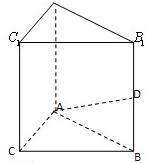
 P是平面ABCD外的点,四边形ABCD是平行四边形,
P是平面ABCD外的点,四边形ABCD是平行四边形,| AB |
| AD |
| AP |
| a |
| b |
| c |
| a |
| b |
| c |
| AB |
| AD |
| AP |
| AB |
| AD |
| AP |
| AP |
| AP |
| AB |
| AD |
| AP |
| AP |
| AB |
| AP |
| AB |
| AP |
| AD |
| AB |
| AD |
| AP |
| AB |
| AD |
| 3 | ||
|
| 1 |
| 3 |
| AB |
| AD |
| AB |
| AD |
| AP |
| AB |
| AD |
| AP |
| AB |
| AD |
| AP |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省杭州十四中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
 =(2,-1,-4),
=(2,-1,-4),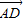 =(4,2,0),
=(4,2,0), =(-1,2,-1).
=(-1,2,-1). =(x1,y1z1),
=(x1,y1z1),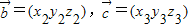 ,定义一种运算:
,定义一种运算: ,试计算
,试计算 的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算
的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算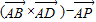 的绝对值的几何意义.
的绝对值的几何意义.
查看答案和解析>>
科目:高中数学 来源:金版人教A版数学理科:立体几何初步6(必修2、选修2-1)(解析版) 题型:解答题
 =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1).
=(-1,2,-1). =(x1,y1z1),
=(x1,y1z1), ,定义一种运算:
,定义一种运算: ,试计算
,试计算 的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算
的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算 的绝对值的几何意义.
的绝对值的几何意义.
查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:7.4 直线、平面平行的判定和性质(1)(解析版) 题型:解答题
 如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH.
如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com