
【题目】如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
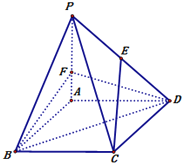
(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.
【答案】(Ⅰ)见解析;(Ⅱ)arctan![]()
【解析】
(Ⅰ)根据线面平行的性质定理进行推理得到E为PD中点即可求PE:ED的值;
(Ⅱ)根据二面角的定义作出二面角的平面角,即可求二面角B﹣DF﹣A的大小.
(Ⅰ)过E作EG∥FD交AP于G,连接CG,连接AC交BD于O,连接FO.
∵EG∥FD,EG面BDF,FD面BDF,∴EG∥面BDF,又EG∩CE=E,CE∥面BDF,EG,CE面CGE,
∴面CGE∥面BDF,又CG面CGE,∴CG∥面BDF,
又面BDF∩面PAC=FO,CG面PAC,∴FO∥CG.
又O为AC中点,∴F为AG中点,且AF=1,∴AF=FG=1,∵PA=3,∴FG=GP=1,
∴E为PD中点,PE:ED=1:1.
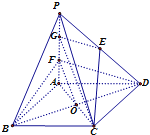
(Ⅱ)过点B作BH⊥直线DA交DA延长线于H,过点H作HI⊥直线DF交DF于I,
∵PA⊥面ABCD,∴面PAD⊥面ABCD,∴BH⊥面PAD,由三垂线定理可得DI⊥IB,
∴∠BIH是二面角B-DF-A的平面角.由题易得AH=![]() ,BH=
,BH=![]() ,HD=
,HD=![]() ,
,
且![]() =
=![]() ,∴HI=
,∴HI=![]() ,∴tan∠BIH=
,∴tan∠BIH=![]() ×
×![]() =
=![]() ,
,
∴二面角B-DF-A的大小为arctan![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
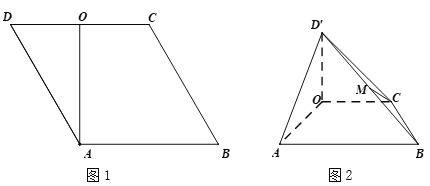
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 上一点(
上一点(![]() 点在第一象限),线段
点在第一象限),线段![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
(1)求线段![]() 的长;
的长;
(2)求椭圆![]() 的离心率;
的离心率;
(3)设直线![]() 交椭圆于
交椭圆于![]() 两点(其中点
两点(其中点![]() 在第一象限),过点
在第一象限),过点![]() 作
作![]() 的平行线
的平行线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为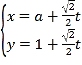 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E为AB的中点.将
,E为AB的中点.将![]() 沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为
沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为![]() .
.
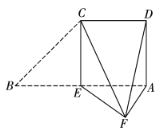
(1)求证:平面![]() 平面AEF;
平面AEF;
(2)求直线DF与平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为6,离心率为
的长轴长为6,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左右焦点分别为![]() ,
,![]() ,左右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且
,左右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记直线AM,BN的斜率分别为
,记直线AM,BN的斜率分别为![]() ,试证明:
,试证明:![]() 的值为定值.
的值为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com