
分析 (1)求出A中不等式的解集确定出A,把m的值代入B确定出B,求出A补集与B的交集即可;
(2)由题意得到B为A的子集,分B为空集与不为空集两种情况求出m的范围即可.
解答 解:(1)集合A={x|x2-3x-10<0}={x|(x+2)(x-5)<0}
={x|-2<x<5},…(2分)
当m=3时,B={x|4≤x≤5};…(3分)
所以∁RA={x|x≤-2或x≥5};…(4分)
所以(∁RA)∩B={x|x=5}={5};…(5分)
(2)因为A∩B=B,所以B⊆A;…(6分)
①当B=∅时,m+1>2m-1,解得m<2,此时B⊆A;…(7分)
②当B≠∅时,应满足$\left\{\begin{array}{l}{m+1≤2m-1}\\{m+1>-2}\\{2m-1<5}\end{array}\right.$,
解得2≤m<3,此时B⊆A;…(9分)
综上所述,m的取值范围是{m|m<3}.…(10分)
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)≥f(b)且当x>0时f(b-x)≥f(b+x) | B. | f(x)≥f(b)且当x>0时f(b-x)≤f(b+x) | ||
| C. | f(x)≥f(a)且当x>0时f(a-x)≥f(a+x) | D. | f(x)≥f(a)且当x>0时f(a-x)≤f(a+x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
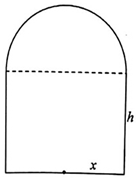 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
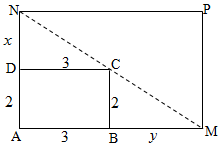 如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.
如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{7}{5}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com