
【题目】已知![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,函数
,函数![]() .
.
(1)设![]() ,
,![]() ,若
,若![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)设![]() ,
,![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(3)设![]() ,
,![]() ,
,![]() ,函数
,函数![]() 的图象是否关于某垂直于
的图象是否关于某垂直于![]() 轴的直线对称?如果是,求出该对称轴,如果不是,请说明理由.
轴的直线对称?如果是,求出该对称轴,如果不是,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)对称轴为
;(2)证明见解析;(3)对称轴为![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据已知条件,将![]() 代入函数
代入函数![]() 的解析式,得出
的解析式,得出![]() ,利用奇函数的定义
,利用奇函数的定义![]() ,可求出实数
,可求出实数![]() 的值;
的值;
(2)判断出函数![]() 和函数
和函数![]() 的单调性,然后利用函数单调性的运算法则,可判断出函数
的单调性,然后利用函数单调性的运算法则,可判断出函数![]() 的单调性,然后利用函数单调性的定义加以证明;
的单调性,然后利用函数单调性的定义加以证明;
(3)根据函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() ,得出
,得出![]() 对任意的实数
对任意的实数![]() 恒成立,即可求出实数
恒成立,即可求出实数![]() 的值.
的值.
(1)由已知,![]() ,
,![]() ,由于函数
,由于函数![]() 为奇函数,
为奇函数,
则![]() 对任意的
对任意的![]() 恒成立,
恒成立,![]() ,因此,
,因此,![]() ;
;
(2)当![]() 时,函数
时,函数![]() 为增函数,函数
为增函数,函数![]() 为减函数,
为减函数,
又![]() ,所以,函数
,所以,函数![]() 在
在![]() 上是增函数,
上是增函数,
下面利用定义来证明出函数![]() 的单调性.
的单调性.
任取![]() ,则
,则![]() ,
,
![]() ,
,![]() ,即
,即![]() ,又
,又![]() ,
,![]() ,
,
![]() ,
,![]() ,所以,
,所以,![]() ,即
,即![]() .
.
因此,函数![]() 在
在![]() 上是增函数;
上是增函数;
(3)![]() ,若函数
,若函数![]() 的图象是轴对称图形,且对称轴为直线
的图象是轴对称图形,且对称轴为直线![]() ,
,
则![]() ,
,![]() ,
,
即![]() ,即
,即![]() ,
,
即![]() 对任意的
对任意的![]() 恒成立,
恒成立,![]() ,即
,即![]() ,
,
因此,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 都是由实数组成的无穷数列.
都是由实数组成的无穷数列.
(1)若![]() 都是等差数列,判断数列
都是等差数列,判断数列![]() 是否是等差数列,说明理由;
是否是等差数列,说明理由;
(2)若![]() ,且
,且![]() 是等比数列,求
是等比数列,求![]() 的所有可能值;
的所有可能值;
(3)若![]() 都是等差数列,数列
都是等差数列,数列![]() 满足
满足![]() ,求证:
,求证: ![]() 是等差数列的充要条件是:
是等差数列的充要条件是: ![]() 中至少有一个是常数.
中至少有一个是常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() ABCD中,
ABCD中,![]() 和
和![]() 都是等边三角形,平面PAD
都是等边三角形,平面PAD![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .
.
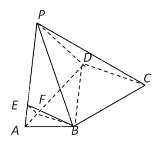
(1)求证:CD![]() PA;
PA;
(2)E,F分别是棱PA,AD上的点,当平面BEF//平面PCD时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iphone手机的年固定成本为40万美元,每生产1万部还需要另外投入16美元,设苹果公司一年内共生产该款iphone手机![]() 万部并全部销售完,每万部的销售收入为
万部并全部销售完,每万部的销售收入为![]() 万元,且
万元,且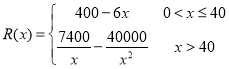 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万部)的函数解析式;
(万部)的函数解析式;
(2)当年产量为多少万部时,苹果公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司最近研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程的测试。现对测试数据进行分析,得到如图所示的频率分布直方图:
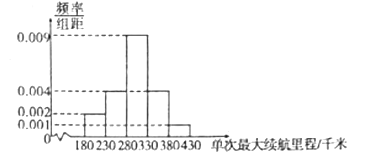
(1)估计这100辆汽车的单次最大续航里程的平均值(同一组中的数据用该组区间的中点值代表).
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程![]() 近似地服从正态分布
近似地服从正态分布![]() ,经计算第(1)问中样本标准差
,经计算第(1)问中样本标准差![]() 的近似值为50。用样本平均数
的近似值为50。用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
参考数据:若随机变量服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券3万元。已知硬币出现正、反面的概率都是0.5方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次。若掷出正面,遥控车向前移动一格(从![]() 到
到![]() )若掷出反面遥控车向前移动两格(从
)若掷出反面遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为P试证明
格的概率为P试证明![]() 是等比数列,并求参与游戏一次的顾客获得优惠券金额的期望值。
是等比数列,并求参与游戏一次的顾客获得优惠券金额的期望值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com