
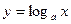 是减函数;已知
是减函数;已知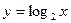 是对数函数,所以
是对数函数,所以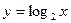 是减函数”,结论显然是错误的,这是因为(***)
是减函数”,结论显然是错误的,这是因为(***) | A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
科目:高中数学 来源:不详 题型:解答题
 ,
, ,求证
,求证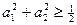 .
. ,
,
 ,恒有
,恒有 ≥0,所以
≥0,所以 ≤0,从而得
≤0,从而得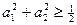 ,
, ,
, ,请写出上述结论的推广式;
,请写出上述结论的推广式;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 .类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________
.类比这一结论,在三棱锥P—ABC中,PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,此三棱锥P—ABC的高为h,则结论为______________查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.矩形都是四边形; | B.四边形的对角线都相等; |
| C.矩形都是对角线相等的四边形; | D.对角线都相等的四边形是矩形 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,平面
,平面 ,且
,且 ,给出下列命题:①若
,给出下列命题:①若 ∥
∥ ,则m⊥
,则m⊥ ;
; ⊥
⊥ ,则m∥
,则m∥ ;③若m⊥
;③若m⊥ ,则
,则 ∥
∥ ;④若m∥
;④若m∥ ,则
,则 ⊥
⊥ 其中正确命题的个数是( )
其中正确命题的个数是( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
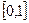 对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标 变成
变成 ,原来的坐标
,原来的坐标 变成1,等等)。则区间
变成1,等等)。则区间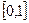 上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是
上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是 ,那么在第
,那么在第 次操作完成后
次操作完成后 ,恰好被拉到与1重合的点对应的坐标是( )
,恰好被拉到与1重合的点对应的坐标是( )
A. 为 为 中所有奇数) 中所有奇数) | B. |
C. 为 为 中所有奇数) 中所有奇数) | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com