
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷(二)(解析版) 题型:填空题
(1)(极坐标与参数方程选做题)在极坐标系中,和极轴垂直且相交的直线l与圆 相交于
相交于 两点,若
两点,若 ,则直线l的极坐标方程为____________.
,则直线l的极坐标方程为____________.
(2)(不等式选做题)不等式 对任意实数
对任意实数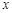 恒成立,则实数
恒成立,则实数 的取值范围是____________.
的取值范围是____________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.存在实数m,使方程x2+mx+1=0没有实数根 |
| B.不存在实数m,使方程x2+mx+1=0没有实数根 |
| C.对任意实数m,使方程x2+mx+1=0没有实数根 |
| D.至多有一个实数m,使方程x2+mx+1=0没有实数根 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨九中高二(上)期末数学试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:201-2012学年福建省厦门六中高三(上)10月月考数学试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com