
【题目】四面体![]() 及其三视图如图所示,过棱
及其三视图如图所示,过棱![]() 的中点
的中点![]() 作平行于
作平行于![]() 、
、![]() 的平面分别交四面体的棱
的平面分别交四面体的棱![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() .
.

(1)求证:四边形![]() 是矩形;
是矩形;
(2)求点![]() 到面
到面![]() 的距离.
的距离.
【答案】(1)详见解析(2)![]()
【解析】
(1)由三视图得到四面体ABCD的具体形状,然后利用线面平行的性质得到四边形EFGH的两组对边平行,即可得到四边形为平行四边形,再由线面垂直的判定和性质得到![]() ,结合异面直线所成角的概念得到
,结合异面直线所成角的概念得到![]() ,从而证得结论;
,从而证得结论;
(2)利用线面平行时,直线上的点到平面的距离是相等的,将点![]() 到面
到面![]() 的距离转化为点D到面
的距离转化为点D到面![]() 的距离,求解即可.
的距离,求解即可.
(1)证明:由 ,同理可得
,同理可得![]()
所以![]()
由 的面,同理可得
的面,同理可得![]()
所以![]()
所以四边形![]() 是平行四边形
是平行四边形
由三视图可知![]() ,所以
,所以![]() ,又
,又![]()
所以![]() ,所以四边形
,所以四边形![]() 是矩形
是矩形
(2)易知![]() 点到面
点到面![]() 的距离即
的距离即![]() 点到面
点到面![]() 的距离,
的距离,
由![]()
所以![]() 点到面
点到面![]() 的距离即
的距离即![]() 点到线
点到线![]() 的距离
的距离
由(1)和![]() 是
是![]() 的中点可知
的中点可知![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
又由三视图可知![]() 是等腰直角三角形,
是等腰直角三角形,
易得![]() 点到线
点到线![]() 的距离为
的距离为![]() ,即
,即![]() 点到面
点到面![]() 的距离
的距离


科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() 为空间中两条互相垂直的直线,等腰直角三角形
为空间中两条互相垂直的直线,等腰直角三角形![]() 的直角边
的直角边![]() 所在直线与
所在直线与![]() ,
,![]() 都垂直,斜边
都垂直,斜边![]() 以直线
以直线![]() 为旋转轴旋转,有下列结论:
为旋转轴旋转,有下列结论:
(1)当直线![]() 与
与![]() 成
成![]() 角时,
角时,![]() 与
与![]() 成
成![]() 角;
角;
(2)当直线![]() 与
与![]() 成
成![]() 角时,
角时,![]() 与
与![]() 成
成![]() 角;
角;
(3)直线![]() 与
与![]() 所成角的最小值为
所成角的最小值为![]() ;
;
(4)直线![]() 与
与![]() 所成角的最小值为
所成角的最小值为![]() ;
;
其中正确的是______(填写所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别是240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动。
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作,求事件M“抽取的2名同学来自同一年级”发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分别直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间![]() 的有8人.
的有8人.

(I)求直方图中![]() 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间![]() 的人数;
的人数;
(II)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取![]() 次.记录如下:
次.记录如下:
甲: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
乙: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(![]() )用茎叶图表示这两组数据.
)用茎叶图表示这两组数据.
(![]() )现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为派哪位学生参加合适?请说明理由.
)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为派哪位学生参加合适?请说明理由.
(![]() )若将频率视为概率,对甲同学在今后的三次数学竞赛成绩进行预测,记这
)若将频率视为概率,对甲同学在今后的三次数学竞赛成绩进行预测,记这![]() 次成绩中高于
次成绩中高于![]() 分的次数为
分的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 轨迹为曲线
轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上关于
上关于![]() 轴对称的两点,点
轴对称的两点,点![]() ,直线
,直线![]() 交曲线
交曲线![]()
于另一点![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
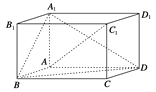
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com