练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知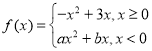函数为奇函数.

    （1）求的值；

    （2）若函数在区间上单调递增，求实数的取值范围.

    （3）当时，求的取值范围.

    【答案】（1）；（2）；（3）见详解.

    【解析】

    （1）求解出在上的解析式即可求解出的值；

    （2）作出的图象，根据图象确定出的单调递增区间，根据是单调递增区间的子集求解出的取值范围；

    （3）根据图象，对进行分类讨论，可求解出的取值范围.

    （1）当时，，所以，

    所以，所以，所以；

    （2）作出如下图所示：

    根据图象可知在上单调递增，因为，

    所以，所以；

    （3）当时即，在上递增，

    所以，，所以；

    当时即，在上递增，

    所以，，所以；

    令，解得或（舍），

    当时即，

    所以在上递增，在上递减，

    所以，，所以；

    当时即，

    所以在上递增，在上递减，

    所以，，所以.

    综上可知：时，；时，；

    时，；时，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥，平面，已知，点，分别为，的中点.

    (1)求证:平面;

    (2)若在线段上，满足平面，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点E、F、G分别是正方体ABCD－A1B1C1D1的棱AB、BC、B1C1的中点，如图所示，则下列命题中的真命题是________(写出所有真命题的编号)．

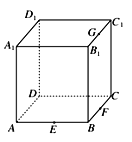
    ①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形；

    ②过点F、D1、G的截面是正方形；

    ③点P在直线FG上运动时，总有AP⊥DE；

    ④点Q在直线BC1上运动时，三棱锥A－D1QC的体积是定值；

    ⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点，则点M的轨迹是一条线段．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为实数）．

    （1）当时，判断函数的单调性，并用定义证明；

    （2）根据的不同取值，讨论的奇偶性，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列有关命题的说法正确的是___（请填写所有正确的命题序号）．

    ①命题“若，则”的否命题为：“若，则”；

    ②命题“若，则”的逆否命题为真命题；

    ③条件，条件，则是的充分不必要条件；

    ④已知时，，若是锐角三角形，则.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数满足，且.

    （1）求函数的解析式；

    （2）求在区间上的最大值和最小值；

    （3）当时，恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动点到定直线的距离比到定点的距离大.

    （1）求动点的轨迹的方程；

    （2）过点的直线交轨迹于， 两点，直线， 分别交直线于点， ，证明以为直径的圆被轴截得的弦长为定值，并求出此定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）求函数的单调区间；

    （Ⅱ）记函数的图象为曲线．设点,是曲线上的不同两点．如果在曲线上存在点，使得：①；②曲线在点处的切线平行于直线，则称函数存在“中值相依切线”．试问：函数是否存在“中值相依切线”，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是边长为4的菱形，且，平面，分别为棱的中点.

    （1）证明：平面.

    （2）若四棱锥的体积为，求点到平面的距离.

    查看答案和解析>>

    同步练习册答案