
【题目】已知函数![]() ,
,![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若对任意的![]() ,都有
,都有![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)函数![]() 的图像上是否存在两点
的图像上是否存在两点![]() ,
,![]() 且
且![]() ,使得直线AB的斜率k满足:
,使得直线AB的斜率k满足:![]() ?若存在,求出
?若存在,求出![]() 与
与![]() 之间的关系;若不存在,请说明理由.
之间的关系;若不存在,请说明理由.
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】十九世纪末:法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”“随机端点”“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设![]() 为圆
为圆![]() 上一个定点,在圆周上随机取一点
上一个定点,在圆周上随机取一点![]() ,连接
,连接![]() ,所得弦长
,所得弦长![]() 大于圆
大于圆![]() 的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个正四面体纸盒的俯视图如图所示,其中四边形ABCD是边长为![]() 的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值是_____.
的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值是_____.
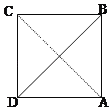
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与抛物线的另一交点分别为两点
与抛物线的另一交点分别为两点![]() 、
、![]() ,连接
,连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 、
、![]() .
.
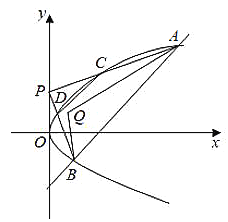
(1)证明:![]() ;
;
(2)若![]() 的面积
的面积![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
(1)若直线![]() 为曲线
为曲线![]() 的一条切线,求实数
的一条切线,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若
,若![]() 在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数
在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,使得平面
同侧折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到图2.
,得到图2.
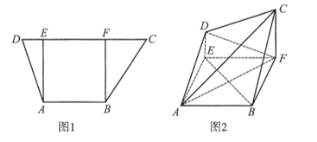
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com