
分析 (1)先求出曲线C1的普通方程,再求C1的极坐标方程.
(2)将直线方程ρcosθ=4化为x=4,设P(x,y),求出点P的轨迹,由此利用弦长公式能求出|AB|.
解答 解:(1)∵方程$\left\{\begin{array}{l}{x=1+t}\\{y=\sqrt{2}t}\end{array}\right.$(t为参数)表示的曲线为C1,
∴曲线C1的普通方程为$\sqrt{2}x-y-\sqrt{2}$=0,
∴C1的极坐标方程为$\sqrt{2}ρcosθ$-ρsinθ-$\sqrt{2}$=0.
(2)以极点为坐标原点建立直角坐标系,将直线方程ρcosθ=4化为x=4,
设P(x,y),Q(4,y0),
∵|OP|•|OQ|=12,∴(x,y)•(4,y0)=12,4x+yy0=12,
又MPO三点共线,xy0=4y,x2+y2-3x=0,
把y=$\sqrt{2}x-\sqrt{2}$代入x2+y2-3x=0,得:3x2-7x+2=0,
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=\frac{7}{3}$,${x}_{1}{x}_{2}=\frac{2}{3}$,
∴|AB|=$\sqrt{(1+2)(\frac{49}{9}-\frac{8}{3})}$=$\frac{5\sqrt{3}}{3}$.
点评 本题考查曲线的极坐标方程和弦长的求法,是基础题,解题时要认真审题,注意弦长公式的合理运用.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {3} | C. | $[{0,\sqrt{3}})$ | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
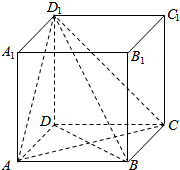 如图,在正方形ABCD-A′B′C′D′,AB=1,
如图,在正方形ABCD-A′B′C′D′,AB=1,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}$π | B. | $\frac{16}{3}$π | C. | 32π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sin2x+cos2x | B. | f(x)=sin2x | C. | f(x)=tan(x+$\frac{π}{8}$) | D. | f(x)=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com