
【题目】如图,在边长为4的菱形![]() 中,
中, ![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上.点
上.点![]() 与点
与点![]() 、
、![]() 不重合,
不重合, ![]() ,
, ![]() ,沿
,沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)记三棱锥![]() 的体积为
的体积为![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,且
,且![]() ,求此时线段
,求此时线段![]() 的长.
的长.
【答案】(1)见解析,(2)![]() .
.
【解析】试题分析:
(1)根据EF⊥AC得PO⊥EF,由平面PEF⊥平面ABEFD结合面面垂直的性质定理,证出PO⊥平面ABEFD,从而得到PO⊥BD.由此结合AO⊥BD,利用线面垂直判定定理即可证出BD⊥平面POA;
(2)由PO⊥平面ABEFD,得PO是三棱锥P﹣ABD和四棱锥P﹣BDEF的高,因此将![]() 化简可得S△ABD=
化简可得S△ABD=![]() S四边形BDEF,从而得到S△CEF=
S四边形BDEF,从而得到S△CEF=![]() S△BCD.最后根据△CEF∽△CDB,利用面积比等于相似比的平方,结合菱形ABCD中有关数据即可算出此时线段PO的长等于
S△BCD.最后根据△CEF∽△CDB,利用面积比等于相似比的平方,结合菱形ABCD中有关数据即可算出此时线段PO的长等于![]() .
.
(Ⅰ)证明:在菱形![]() 中,∵
中,∵![]() ,∴
,∴![]() . ∵
. ∵![]() ,∴
,∴![]() ,
,
∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,且
,且![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() , ∵
, ∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)设![]() .由(Ⅰ)知,
.由(Ⅰ)知, ![]() 平面
平面![]() ,
,
∴![]() 为三棱锥
为三棱锥![]() 及四棱锥
及四棱锥![]() 的高,
的高,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ∽
∽![]() . ∴
. ∴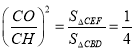 ,
,
∴![]() , ∴
, ∴![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+2)与g(x)=(x﹣a)2+1,若对任意的x1∈[2,6),都存在x2∈[0,2],使得f(x1)=g(x2),则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得 M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=m. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)都是定义在R上的函数,且满足以下条件:
①f(x)=axg(x)(a>0,a≠1);
②g(x)≠0;
③f(x)g'(x)>f'(x)g(x);
若 ![]() ,则a= .
,则a= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占![]() ,女生中喜欢数学课程的占
,女生中喜欢数学课程的占![]() ,得到如下列联表.
,得到如下列联表.
喜欢数学课程 | 不喜欢数学课程 | 合计 | |
男生 | |||
女生 | |||
合计 |
(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;
(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,求抽取的学生中至少有1名是女生的概率..
附:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图(图1)及三视图(图2)如图所示,其中M,N分别是AF,BC的中点 
(1)求证:MN∥平面CDEF:
(2)求二面角A﹣CF﹣B的余弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com