
分析 (Ⅰ)求出直线斜率,即可求入射光线和反射光线所在的直线方程;
(Ⅱ)l⊥MN时,M到l的距离最大,求出l的方程,再求出圆心与半径,即可求出圆的方程.
解答 解:(Ⅰ)∵kPQ=-$\sqrt{3}$,∴l1:y=-$\sqrt{3}$(x-2),
∵l1,l2关于x轴对称,
∴l2:y=$\sqrt{3}$(x-2);
(Ⅱ)设M到直线l的距离为MH,
∵l恒过点N(-2$\sqrt{3}$,0),∴MH=$\sqrt{48-N{H}^{2}}$,
∴NH=0时,MH最大,即l⊥MN时,M到l的距离最大,
∵kMN=-$\sqrt{3}$,∴m=$\sqrt{3}$,
∴l的方程为x=$\sqrt{3}$y-2$\sqrt{3}$,
设所求方程为(x-2)2+(y-t)2=r2,∴r=$\frac{|t|}{2}$=$\frac{|\sqrt{3}t-2\sqrt{3}-2|}{2}$,∴t=2(另一根舍去),
∴所求方程为(x-2)2+(y-2)2=1.
点评 本题考查直线与圆的方程,考查点到直线距离公式的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | $-\frac{12}{13}$ | C. | $\frac{12}{13}$ | D. | $-\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{2}$或$\frac{8}{5}$ | D. | $\frac{5}{2}$或$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
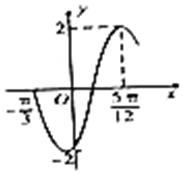 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
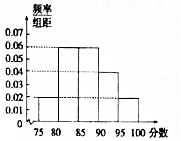 某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com