
| a |
| b |
| A、-6和10 |
| B、6和-10 |
| C、-6和-10 |
| D、6和10 |
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
A、7
| ||
B、6
| ||
C、4
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 用电量(单位:千瓦时) | 用电价格(单位:元/千瓦时) | |
| 第一档 | 180及以下部分 | 0.57 |
| 第二档 | 超180至400部分 | 0.62 |
| 第三档 | 超400部分 | 0.87 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若m∥n,n?α则 m∥α |
| B、若m?α,α⊥β,则m⊥β |
| C、若m∥n,m⊥α,则n⊥α |
| D、若m⊥n,m?α,n?β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、(-∞,-2] |
| B、(-3,-1) |
| C、[-1,0) |
| D、[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
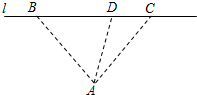 某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=
某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| e |
| c |
| a |
A、[1,
| ||
| B、[1,+∞) | ||
| C、(-∞,e-1] | ||
| D、[1,e-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com