
理科(本小题14分)已知函数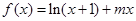 ,当
,当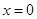 时,函数
时,函数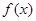 取得极大值.
取得极大值.
(Ⅰ)求实数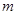 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数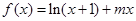 在区间
在区间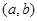 内导数都存在,且
内导数都存在,且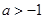 ,则存在
,则存在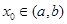 ,使得
,使得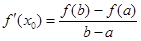 .试用这个结论证明:若
.试用这个结论证明:若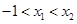 ,函数
,函数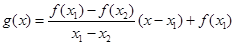 ,则对任意
,则对任意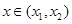 ,都有
,都有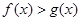 ;(Ⅲ)已知正数
;(Ⅲ)已知正数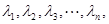 满足
满足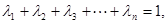 求证:当
求证:当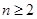 ,
,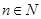 时,对任意大于
时,对任意大于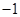 ,且互不相等的实数
,且互不相等的实数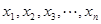 ,都有
,都有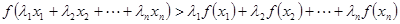
(Ⅰ)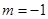 .
.
(Ⅱ)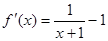
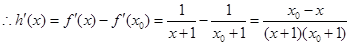
当 时,
时,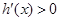 ,
,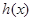 单调递增,
单调递增,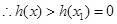 ;
;
当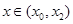 时,
时, ,
,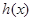 单调递减,
单调递减,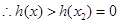 ;(Ⅲ)用数学归纳法证明.
;(Ⅲ)用数学归纳法证明.
【解析】
试题分析:(Ⅰ) . 由
. 由 ,得
,得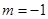 ,此时
,此时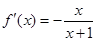 .
.
当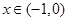 时,
时, ,函数
,函数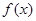 在区间
在区间 上单调递增;
上单调递增;
当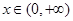 时,
时,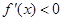 ,函数
,函数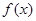 在区间
在区间 上单调递减.
上单调递减.
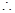 函数
函数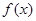 在
在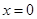 处取得极大值,故
处取得极大值,故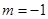 .
3分
.
3分
(Ⅱ)令 , 4分
, 4分
则 .函数
.函数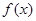 在
在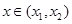 上可导,
上可导,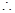 存在
存在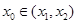 ,使得
,使得 .
.
又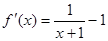

当 时,
时,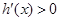 ,
,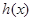 单调递增,
单调递增,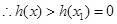 ;
;
当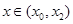 时,
时, ,
,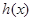 单调递减,
单调递减,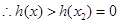 ;
;
故对任意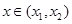 ,都有
,都有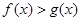 .
8分
.
8分
(Ⅲ)用数学归纳法证明.
①当 时,
时, ,且
,且 ,
,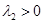 ,
,
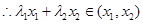 ,
,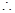 由(Ⅱ)得
由(Ⅱ)得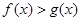 ,即
,即
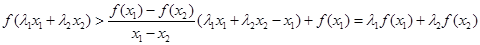 ,
,
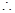 当
当 时,结论成立. 9分
时,结论成立. 9分
②假设当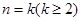 时结论成立,即当
时结论成立,即当 时,
时,
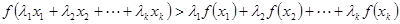 . 当
. 当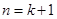 时,设正数
时,设正数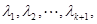 满足
满足 令
令 ,
,

则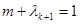 ,且
,且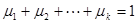 .
.


13分
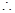 当
当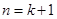 时,结论也成立.
时,结论也成立.
综上由①②,对任意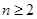 ,
,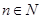 ,结论恒成立. 14分
,结论恒成立. 14分
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性、最值及不等式的证明,数学归纳法。
点评:难题,利用导数研究函数的单调性、极值、最值,是导数的应用中的基本问题。本题(III)应用数学归纳法证明不等式,难度较大。涉及对数函数,要特别注意函数的定义域。


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
(本小题满分14分)
已知点P ( t , y )在函数f ( x ) = ![]() (x ?? –1)的图象上,且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).
(x ?? –1)的图象上,且有t2 – c2at + 4c2 = 0 ( c ?? 0 ).
(1) 求证:| ac | ?? 4;(2) 求证:在(–1,+∞)上f ( x )单调递增.(3) (仅理科做)求证:f ( | a | ) + f ( | c | ) > 1.
查看答案和解析>>
科目:高中数学 来源:2014届江西南昌八一、洪都、麻丘中学高二上期中数学试卷(解析版) 题型:解答题
(本小题满分14分)(理科)已知椭圆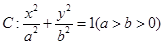 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点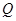
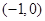 的直线
的直线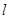 交椭圆于
交椭圆于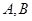 两点,交直线
两点,交直线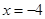 于点
于点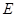 ,且
,且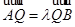 ,
,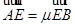 ,
,
求证: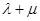 为定值,并计算出该定值.
为定值,并计算出该定值.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高二上学期期中考试数学卷 题型:解答题
(本小题满分14分) 已知数列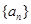 和
和 满足:
满足: ,
, ,
, ,
, (
( ),且
),且 是以
是以 为公比的等比数列.
为公比的等比数列.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
(Ⅲ)(理科做,文科不做)若 ,求和:
,求和: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考四川卷理科22) (本小题满分14分)
已知![]() 为正实数,
为正实数,![]() 为自然数,抛物线
为自然数,抛物线![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,设
,设![]() 为该抛物线在点
为该抛物线在点![]() 处的切线在
处的切线在![]() 轴上的截距。
轴上的截距。
(Ⅰ)用![]() 和
和![]() 表示
表示![]() ;
;
(Ⅱ)求对所有![]() 都有
都有![]() 成立的
成立的![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com