分析:(1)设
A(x1,),
B(x2,),由曲线8y=x
2上任意一点斜率为y'=
,由已知,A,B,F三点共线,设直线AB的方程为:y=kx+2与抛物线方程x
2=8y联立消y,从而得解;
(2)先求得
和
,进而可求得
•的结果为0,
(3)先求得∵
=(,-2-),∵
=(,-2-),从而可解.
解答:解:(1)设
A(x1,),
B(x2,),由曲线8y=x
2上任意一点斜率为y'=
,
直线AM的方程为:
y-=(x-x1)直线BM的方程为:
y-=(x-x2) 解方程组得
x=,y= 即
M(,)由已知,A,B,F三点共线,设直线AB的方程为:y=kx+2
与抛物线方程x
2=8y联立消y可得:x
2-8kx-16=0,∴x
1+x
2=8k,x
1x
2=-16
所以M点的纵坐标为-2,,所以线段FM中点的纵坐标为0
即线段FM被x轴平分.
(2)
=(4k,-4),=(x2-x1,),
∴
•=4k(x2-x1)-=(x2-x1)(4k-)由(1)x
1+x
2=8k,代入得
•=0(3)∵
=(,-2-),∵
=(,-2-),
∴
•=+4+=-8+4+4=0∴
⊥ 点评:本题主要考查了抛物线的应用.抛物线与直线的关系和抛物线的性质等都是近几年高考的热点,故应重点掌握.

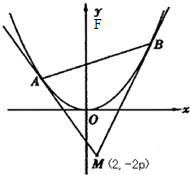 已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且

 名校课堂系列答案
名校课堂系列答案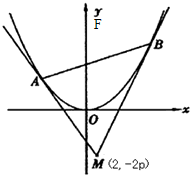 已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且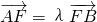 (λ>0),
(λ>0),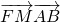 的值;
的值;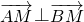 .
.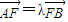 (λ>0),
(λ>0),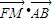 的值;
的值;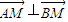 .
.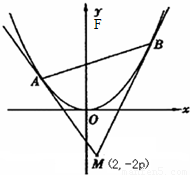
 ,过A、B两点分别作抛物线的切线,设其交点为M
,过A、B两点分别作抛物线的切线,设其交点为M 的值;
的值;