
【题目】已知函数 ![]() ,x∈R.
,x∈R.
(1)证明对a、b∈R,且a≠b,总有:|f(a)﹣f(b)|<|a﹣b|;
(2)设a、b、c∈R,且 ![]() ,证明:a+b+c≥ab+bc+ca.
,证明:a+b+c≥ab+bc+ca.
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】以下关于线性回归的判断,正确的个数是( )

①若散点图中所有点都在一条直线附近,则这条直线为回归直线;
②散点图中的绝大多数都线性相关,个别特殊点不影响线性回归,如图中的A,B,C点;
③已知直线方程为![]() =0.50x-0.81,则x=25时,y的估计值为11.69;
=0.50x-0.81,则x=25时,y的估计值为11.69;
④回归直线方程的意义是它反映了样本整体的变化趋势.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
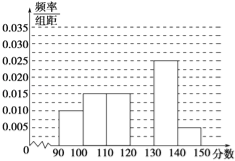
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测技改后生产100吨甲产品比技改前少消耗多少吨标准煤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x(ex﹣1)﹣ax2(e=2.71828…是自然对数的底数).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)若f(x)在(﹣1,0)内无极值,求a的取值范围;
(3)设n∈N* , x>0,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( ) 
A.![]() (a>0,b>0)
(a>0,b>0)
B.a2+b2≥2ab(a>0,b>0)
C.![]() (a>0,b>0)
(a>0,b>0)
D.![]() (a>0,b>0)
(a>0,b>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(![]() ,1),直线l的参数方程为
,1),直线l的参数方程为 (t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=
(t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=![]() cos(θ-
cos(θ-![]() )
)
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|﹣|x﹣3|.
(Ⅰ)解不等式f(x)≥1;
(Ⅱ)当﹣9≤x≤4时,不等式f(x)<a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣2cosx﹣x+(x+1)ln(x+1),g(x)=k(x2+ ![]() ).其中k≠0.
).其中k≠0.
(1)讨论函数g(x)的单调区间;
(2)若存在x1∈(﹣1,1],对任意x2∈( ![]() ,2],使得f(x1)﹣g(x2)<k﹣6成立,求k的取值范围.
,2],使得f(x1)﹣g(x2)<k﹣6成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com