
在△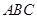 中,角
中,角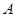 、
、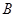 、
、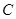 所对的边长分别为
所对的边长分别为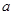 、
、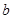 、
、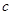 ,
,
且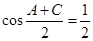 .
.
(1)若 ,
,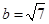 ,求
,求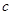 的值;
的值;
(2)若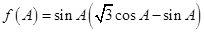 ,求
,求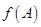 的取值范围.
的取值范围.
(1)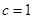 或
或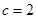 ;(2)
;(2)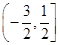
 .
.
解析试题分析:(1)已知两边,要求第三边,最好能求出已知两边的夹角,然后用余弦定理可求得,而由已知条件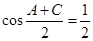 可得
可得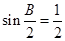 ,从而可知
,从而可知 ,即
,即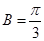 ,问题得解;(2)这是三角函数的一般性问题,解决它的一般方法是把函数化为
,问题得解;(2)这是三角函数的一般性问题,解决它的一般方法是把函数化为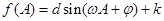 的形式,然后利用正弦函数的知识解决问题,
的形式,然后利用正弦函数的知识解决问题,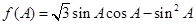 ,首先用二倍角公式,降幂公式把二次式化为一次式
,首先用二倍角公式,降幂公式把二次式化为一次式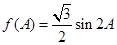

 ,再利用两角和的正弦公式把两个三角函数化为一个三角函数,
,再利用两角和的正弦公式把两个三角函数化为一个三角函数,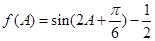 ,接下来我们只要把
,接下来我们只要把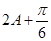 作为一个整体,求出它的范围,就可借助于正弦函数求出
作为一个整体,求出它的范围,就可借助于正弦函数求出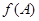 的取值范围了.
的取值范围了.
试题解析:(1)在△ 中,
中, .
.
所以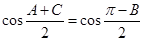
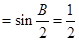 .
. ,所以
,所以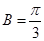 . 3分
. 3分
由余弦定理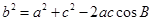 ,得
,得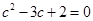 .
.
解得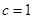 或
或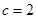 . 6分
. 6分
(2)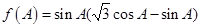

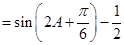 . 9分
. 9分
由(1)得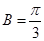 ,所以
,所以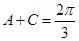 ,
,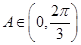 ,
,
则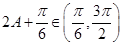 .
.
∴ .∴
.∴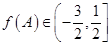 .
.
∴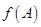 的取值范围是
的取值范围是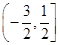 . 12分
. 12分
考点:(1)余弦定理;(2)二倍角公式与降幂公式,三角函数的取值范围


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
若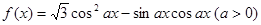 的图像与直线
的图像与直线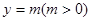 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为 的等差数列.
的等差数列.
(1)求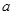 和
和 的值;
的值;
(2)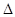 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若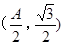 是函数
是函数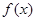 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求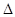 ABC面积的最大值.
ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.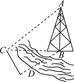
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com