
【题目】数列{an}的前n项和Sn满足 ![]() ,且a1 , a2+6,a3成等差数列.
,且a1 , a2+6,a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)由 ![]() ,再写一式,两式相减,可得an=
,再写一式,两式相减,可得an= ![]() an﹣
an﹣ ![]() an﹣1 , 即an=3an﹣1 .
an﹣1 , 即an=3an﹣1 .
由a1 , a2+6,a3成等差数列,得2(a2+6)=a1+a3 , 解得a1=3.
故数列{an}是以3为首项,3为公比的等比数列,所以an=3n .
(Ⅱ)an+1=3n+1 , Sn= ![]() ,则Sn+1=
,则Sn+1= ![]() .
.
bn= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
所以数列{bn}的前n项和Tn= ![]() [(
[( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )]=
)]= ![]() (
( ![]() ﹣
﹣ ![]() )
)
【解析】(Ⅰ)由 ![]() ,再写一式,两式相减,可得an=
,再写一式,两式相减,可得an= ![]() an﹣
an﹣ ![]() an﹣1 , 即an=3an﹣1 . 由a1 , a2+6,a3成等差数列,得2(a2+6)=a1+a3 , 解得a1=3,即可求数列{an}的通项公式;(Ⅱ)设bn=
an﹣1 , 即an=3an﹣1 . 由a1 , a2+6,a3成等差数列,得2(a2+6)=a1+a3 , 解得a1=3,即可求数列{an}的通项公式;(Ⅱ)设bn= ![]() ,确定通项,利用裂项法求数列{bn}的前n项和Tn .
,确定通项,利用裂项法求数列{bn}的前n项和Tn .
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系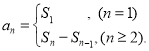 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若椭圆
,若椭圆![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点,且线段
两点,且线段![]() 恰好为圆
恰好为圆![]() 的直径.
的直径.
(1)求直线![]() 的方程;
的方程;
(2)求椭圆![]() 的标准方程.
的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,AB=5,AC=12,BC=13,一只小蚂蚁从△ABC的内切圆的圆心处开始随机爬行,当蚂蚁(在三角形内部)与△ABC各边距离不低于1个单位时其行动是安全的,则这只小蚂蚁在△ABC内任意行动时安全的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() .
.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若函数f(x)存在极值,对于任意的0<x1<x2 , 存在正实数x0 , 使得f(x1)﹣f(x2)=f'(x0)(x1﹣x2),试判断x1+x2与2x0的大小关系并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() .过
.过![]() 作一个平面
作一个平面![]() 使得
使得![]() 平面
平面![]() .
.
(1)求平面![]() 将四棱锥
将四棱锥![]() 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;
(2)若平面![]() 与平面
与平面![]() 之间的距离为
之间的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]()
![]() 平面
平面![]() ,且四边形
,且四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(I)求证: ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 是线段
是线段![]() 上的动点,当直线
上的动点,当直线![]() 与
与![]() 所成角最小时,求线段
所成角最小时,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com