
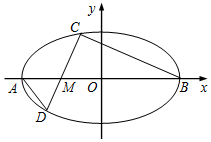
 ��ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����������ֱ�ΪA��-a��0����B��a��0������M��-1��0������3$\overrightarrow{AM}$=$\overrightarrow{MB}$������Mб��Ϊk��k��0����ֱ�߽���ԲE��C��D���㣬���е�C��x���Ϸ���
��ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����������ֱ�ΪA��-a��0����B��a��0������M��-1��0������3$\overrightarrow{AM}$=$\overrightarrow{MB}$������Mб��Ϊk��k��0����ֱ�߽���ԲE��C��D���㣬���е�C��x���Ϸ������� ��1����3$\overrightarrow{AM}$=$\overrightarrow{MB}$����a ���ɣ�
��2�����C������Ϊ��x0��y0����y0��0����BC��CD���ã�-1-x0���� 2-x0��+y02=0�����x0=-$\frac{2}{3}$��y0=$\frac{2\sqrt{2}}{3}$�����ɣ�
��3������C��x0��y0������CD��y=$\frac{{y}_{0}}{{x}_{0}+1}$��x+1����-2��x0��2��x0��-1����
��$\left\{\begin{array}{l}y=\frac{y0}{x0+1}��x+1��\\ \frac{x2}{4}+y2=1\end{array}$��ȥy����x2+8y02x+4y02-4��x0+1��2=0����D��$\frac{-8-5{x}_{0}}{5+2{x}_{0}}$��$\frac{-3{y}_{0}}{5+2{x}_{0}}$��������$\frac{{k}_{1}}{{k}_{2}}$
��� �⣺��1����Ϊ3$\overrightarrow{AM}$=$\overrightarrow{MB}$������3��-1+a��0��=��a+1��0�������a=2�� ����2�֣�
����Ϊ$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$������c=$\sqrt{3}$������b2=a2-c2=1��
������ԲE�ķ���Ϊ$\frac{x2}{4}$+y2=1�� ����4�֣�
��2�����C��������x0��y0����y0��0��
��$\overrightarrow{CM}$=��-1-x0��-y0����$\overrightarrow{CB}$=��2-x0��-y0����
��ΪBC��CD�����ԣ�-1-x0���� 2-x0��+y02=0�� �١���6�֣�
����Ϊ$\frac{{{x}_{0}}^{2}}{4}$+y02=1����
�����٢ڣ����x0=-$\frac{2}{3}$��y0=$\frac{2\sqrt{2}}{3}$������8�֣�
����k=$\frac{\frac{2\sqrt{2}}{3}}{-\frac{2}{3}+1}$=2$\sqrt{2}$�� ����10�֣�
��3������C��x0��y0������CD��y=$\frac{{y}_{0}}{{x}_{0}+1}$��x+1����-2��x0��2��x0��-1����
��$\left\{\begin{array}{l}y=\frac{y0}{x0+1}��x+1��\\ \frac{x2}{4}+y2=1\end{array}$��ȥy��
��x2+8y02x+4y02-4��x0+1��2=0������12�֣�
����Ϊ$\frac{{{x}_{0}}^{2}}{4}$+y02=1�����Ե�D��$\frac{-8-5{x}_{0}}{5+2{x}_{0}}$��$\frac{-3{y}_{0}}{5+2{x}_{0}}$��������14�֣�
����$\frac{{k}_{1}}{{k}_{2}}$=$\frac{\frac{-3{y}_{0}}{5+2{y}_{0}}}{\frac{-8-5{x}_{0}}{5+2{x}_{0}}}•\frac{{x}_{0}-2}{{y}_{0}}$=$\frac{-3{y}_{0}}{-{x}_{0}+2}•\frac{{x}_{0}-2}{{y}_{0}}$=3��
����$\frac{k1}{k2}$Ϊ��ֵ�� ����16�֣�
���� ���⿼����ֱ����Բ��λ�ù�ϵ���Լ���������Ҫ��ϸߣ���������̵�˼��ᴩ����������̣������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��2��3�� | C�� | ��-2��-1���ȣ�1��+�ޣ� | D�� | ��0��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{4}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com