
(19) (本小题满分12分)某厂家根据以往的经验得到有关生产销售规律如下:每生产![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本
(万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本![]() 固定成本
固定成本![]() 生产成本);销售收入
生产成本);销售收入![]() (万元)满足:
(万元)满足: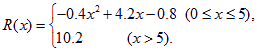 (Ⅰ)要使工厂有盈利,求
(Ⅰ)要使工厂有盈利,求![]() 的取值范围;
的取值范围;
(Ⅱ)求生产多少台时,盈利最多?
科目:高中数学 来源: 题型:
19(本小题满分12分)
P是以![]() 为焦点的双曲线C:
为焦点的双曲线C:![]() (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知![]() =0,
=0,![]() .
.
(1)试求双曲线的离心率![]() ;
;
(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当![]() ,
,![]() = 0,求双曲线的方程.
= 0,求双曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
19(本小题满分14分)已知f(x)=2x-1的反函数为![]() (x),g(x)=log4(3x+1).(1)若f-1(x)≤g(x),求x的取值范围D;(2)设函数H(x)=g(x)-
(x),g(x)=log4(3x+1).(1)若f-1(x)≤g(x),求x的取值范围D;(2)设函数H(x)=g(x)-![]() (x),当x∈D时,求函数H(x)的值域.
(x),当x∈D时,求函数H(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
19(本小题满分14分)已知![]() ,函数
,函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).(1)求函数
为自然对数的底数).(1)求函数![]() 在区间
在区间![]() 上的最小值;(2)是否存在实数
上的最小值;(2)是否存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直? 若存在,求出
轴垂直? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二(奥赛班)上学期期中考试数学 题型:解答题
19(本小题满分13分)
随机抽取某中学甲乙两班各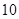 名同学,测量他们的身高(单位:
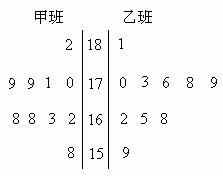
名同学,测量他们的身高(单位: 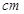 ),获得身高数据的茎叶图如下图:
),获得身高数据的茎叶图如下图:
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
 (3)现从乙班这
(3)现从乙班这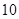 名同学中随机抽取两名身高不低于
名同学中随机抽取两名身高不低于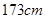 的同学,求身高为
的同学,求身高为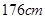 的同学被抽中的概率。
的同学被抽中的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com