
【题目】2016年巴西奥运会的周边商品有80%左右为“中国制造”,所有的厂家都是经过层层筛选才能获此殊荣.甲、乙两厂生产同一产品,为了解甲、乙两厂的产品质量,以确定这一产品最终的供货商,采用分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件,测量产品中的微量元素的含量(单位:毫克).下表是从乙厂抽取的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 169 | 178 | 166 | 175 | 180 |
| 75 | 80 | 77 | 70 | 81 |
(1)求乙厂生产的产品数量:
(2)当产品中的微量元素![]() 满足:
满足:![]() ,且
,且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数的分布列及数学期望.
【答案】(1)35(2)14(3)![]()
【解析】
试题分析:(1)根据分层抽样得乙厂生产的产品总数为![]() (2)由频率估计概率得乙厂样品中优等品的频率为
(2)由频率估计概率得乙厂样品中优等品的频率为![]() ,因此乙厂生产的优等品的数量为
,因此乙厂生产的优等品的数量为![]() (3)先确定随机变量取法
(3)先确定随机变量取法![]() ,再分别求对应概率:
,再分别求对应概率:![]() ,列表可得分布列,根据公式可求数学期望
,列表可得分布列,根据公式可求数学期望![]()
试题解析:(1)乙厂生产的产品总数为![]() ;...................3分
;...................3分
(2)样品中优等品的频率为![]() ,乙厂生产的优等品的数量为
,乙厂生产的优等品的数量为![]() ;...........6分
;...........6分
(3)![]() .
.
![]() ,.....................8分
,.....................8分
![]() 的分布列为
的分布列为
| 0 | 1 | 2 |
|
|
|
|
...........................................11分
均值![]() ...............................12分
...............................12分


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为![]() ,求△AOB面积的最大值,并求此时直线l的方程.
,求△AOB面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间 | 2014年下半年 | 2015年上半年 | 2015年下半年 | 2016年上半年 | 2016年下半年 |
时间代号 |
|
|
|
|
|
人均读书量 |
|
|
|
|
|
根据散点图,可以判断出人均读书量![]() 与时间代号
与时间代号![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
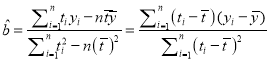 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() 和点
和点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线方程.
的切线,求切线方程.
(3)设直线![]() ,且直线
,且直线![]() 被圆
被圆![]() 所截得的弦为
所截得的弦为![]() ,满足
,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)设该公司从至少消费两次, 求这的顾客消费次数用分层抽样方法抽出![]() 人, 再从这
人, 再从这![]() 人中抽出
人中抽出![]() 人发放纪念品, 求抽出
人发放纪念品, 求抽出![]() 人中恰有
人中恰有![]() 人消费两次的概率.
人消费两次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过右焦点和短轴一个端点的直线的斜率为
的焦距为2,过右焦点和短轴一个端点的直线的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记
两点,记![]() 面积的最大值为
面积的最大值为![]() ,证明:
,证明: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两条不同直线,
是两条不同直线, ![]() 、
、![]() 是两个不同平面,则下列四个命题:
是两个不同平面,则下列四个命题:
① 若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
② 若![]() ,
, ![]() ,则
,则![]() ;
;
③ 若![]() ,
, ![]() ,则
,则![]() 或
或![]() ;
;
④ 若![]() ,
, ![]() ,
, ![]() ,则
,则![]() .
.
其中正确命题的个数为 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com