
如图,若射线 上分别存在点
上分别存在点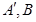 与
与 ,则三角形面积之比
,则三角形面积之比  ,如图若不在同一平面内的射线
,如图若不在同一平面内的射线 和
和 上分别存在点
上分别存在点 点
点 和点
和点 ,则三棱锥体积之比
,则三棱锥体积之比 

科目:高中数学 来源: 题型:填空题
n个连续自然数按规律排成下表:
0 3 → 4 7 → 8 11 …
↓ ↑ ↓ ↑ ↓ ↑
1 → 2 5 → 6 9 → 10
根据规律,从2 009到2 011的箭头方向依次为________.
①↓→ ②→↑ ③↑→ ④→↓
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在平面几何里,已知直角三角形ABC中,角C为
 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
有三角形的勾股定理,给出空间中三棱锥的有关结论:________
若三角形ABC的外接圆的半径为 ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S=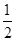 r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,推广到第 个等式为
个等式为
_________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com