
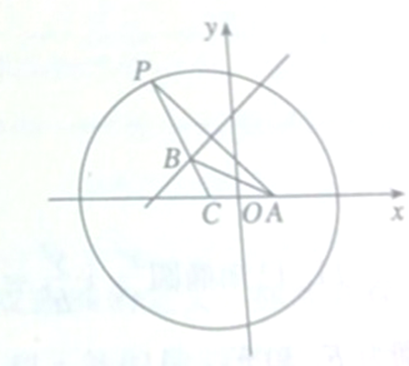
 如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.
如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.| x2 |
| 4 |
| y2 |
| 3 |


科目:高中数学 来源: 题型:
 如图所示,为了测量某湖泊两侧A,B间的距离,某同学首先选定了与A,B不共线的一点C,然后给出了四种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c)
如图所示,为了测量某湖泊两侧A,B间的距离,某同学首先选定了与A,B不共线的一点C,然后给出了四种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c)| A、①②③ | B、②③④ |
| C、①③④ | D、①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,0) | ||
D、[0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、在△ABC中,A>B是sinA>sinB的充要条件 |
| B、在锐角△ABC中,不等式sinA>cosB恒成立 |
| C、在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形 |
| D、在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com